比特幣會歸零嗎？

比特幣

比特幣發展至今已歷經十年，「十年之前，我不認識你，你不屬於我」，那麼，十年之後，我們和比特幣還是不是朋友?還是不是可以問候?還是那種溫柔再也找不到擁抱的理由了呢?

這段時間，很多朋友來問比特幣會不會歸零的問題。其中不乏高位入場的朋友，也有認為跌了差不多了想入市的新人，也有糾結在關機還是堅持挖礦兩難之中的礦圈朋友。

前兩天一直在寫《Web3.0：能否開啟未來10年創新創業創富的大門》文章，完成後發現有必要寫篇文章討論下這個話題。

無論是鏈圈、幣圈還是礦圈，有很多充值比特幣信仰的文章。但筆者發現，很少有從比特幣的白皮書和算法層面來解釋的，本文希望能填補上這塊。

本文將分四部分：

第一部分，解讀《密碼朋克宣言》與比特幣白皮書。

沒有密碼朋克運動就沒有當代基於密碼學的各種點對點網路產品與算法突破，更不用說比特幣。解讀《密碼朋克宣言》對正確理解比特幣的產生原因非常重要。其次，解讀比特幣白皮書的文章有很多，但似乎沒有看到過對中本聰這篇論文的開頭簡介部分和結尾的結論部分做深度刨析的。搞學術的朋友都知道，這兩部分常常是最重要的畫龍點睛部分。不深刻解讀這兩部分，很可能會片面的理解比特幣。

第二部分，解讀比特幣的自治機制。

筆者曾解讀源碼並推導出了一個非常簡單的比特幣挖礦成本公式，由此公式推導出了基於比特幣自治機制的分布式商業理論。這部分將根據這個公式來解讀為什麼比特幣能成為打不死的小強。

第三部分，談談支持比特幣價格上漲的7個理由。

第四部分，談談比特幣可能歸零的幾個條件。

因為篇幅關係，以上四部分將分為兩篇文章講述。

以下是正文：

01

起源與原理

1993年發布的《密碼朋克宣言》篇幅不長，提出的核心訴求是如何在互聯網上保護用戶隱私。以下文字摘自此《宣言》：

由於我們渴望隱私，我們必須確保交易各方只知道該交易需要的信息。既然任何信息都可以被提及，我們必須確保盡可能少地披露。

在大多數情況下，個人身份並不重要。當我在商店里買了一本雜誌，然後把現金交給店員時，就不需要知道我是誰了。當我要求我的電子郵件提供者發送和接收信息時，我的提供者不需要知道我在對誰說話，我在說什麼，或者其他人對我說什麼;我的供應商只需要知道如何在得到商品，以及我欠他們多少錢。當我的身份被交易的潛在機制暴露時，我就沒有隱私了。我不能選擇性地暴露我自己;我必須始終在暴露我自己的同時，保護我的隱私。

因此，開放社會中的隱私要求匿名交易系統。到目前為止，現金一直是主要的此類系統。

匿名事務系統不是秘密事務系統。匿名系統授權個人在需要時和僅在需要時披露其身份-這就是隱私的本質。

在開放社會中，隱私也需要加密。如果我說了什麼，我只想讓我想聽的人聽到。如果我的演講內容可以向全世界公開，我就沒有隱私了。加密表示對隱私的渴望，而用弱加密表示對隱私的渴望不大。此外，在默認為匿名的情況下，要想安全地顯示身份，需要加密簽名。

我們這些密碼朋克致力於建立匿名系統。我們用密碼學、匿名電子郵件系統、數字簽名和數字貨幣來捍衛我們的隱私。

密碼朋克積極致力於使網路更安全，保護隱私。讓我們一起趕緊行動，團結起來!

這份25年前的《宣言》明確提出了：要用數字簽名和數字貨幣來捍衛隱私。

這也可以看作是密碼朋克運動的使命之一。1993年之後，該組織中的重要人物 Wei Dai、David Chaum、Adam Back、Nick Sazbo、Hal Finney等人在數字貨幣技術上相繼做出了非常傑出的探索，最終2008年由中本聰集大成，推出了點對點網路上的電子現金系統解決方案，即：比特幣。

接下去來看比特幣白皮書的簡介，內容如下：

互聯網上的貿易，幾乎都需要借助金融機構作為可資信賴的第三方來處理電子支付信息。雖然這類系統在絕大多數情況下都運作良好，但是這類系統仍然內生性地受制於「基於信用的模式」(trust based model)的弱點。我們無法做到完全不可逆的交易，因為金融機構總是不可避免地會出面協調爭端。而金融中介的存在，也會增加交易的成本，並且限制了實際可行的最小交易規模，也限制了日常的小額支付交易。並且潛在的損失還在於，很多商品和服務本身是無法退貨的，如果缺乏不可逆的支付手段，互聯網的貿易就大大受限。因為有潛在的退款的可能，就需要交易雙方擁有信任。而商家也必須提防自己的客戶，因此會向客戶索取完全不必要的個人信息。而實際的商業行為中，一定比例的欺詐性客戶也被認為是不可避免的，相關損失視作銷售費用處理。而在使用物理現金的情況下，這些銷售費用和支付問題上的不確定性卻是可以避免的，因為此時沒有第三方信用中介的存在。 所以，我們非常需要這樣一種電子支付系統，它基於密碼學原理而不基於信用，使得任何達成一致的雙方，能夠直接進行支付，從而不需要第三方中介的參與。杜絕回滾(reverse)支付交易的可能，這就可以保護特定的賣家免於欺詐;而對於想要保護買家的人來說，在此環境下設立通常的第三方擔保機制也可謂輕鬆加愉快。在這篇論文中，我們(we)將提出一種通過點對點分布式的時間戳服務器來生成依照時間前後排列並加以記錄的電子交易證明，從而解決雙重支付問題。只要誠實的節點所控制的計算能力的總和，大於有合作關係的(cooperating)攻擊者的計算能力的總和，該系統就是安全的。

從這段文字中可以看出，中本聰開發比特幣的初心來源於以下幾點：

1、現有的中心化信任機制存在嚴重缺陷，包括：

交易的可逆性或回滾(Reverse)會給買賣雙方造成潛在風險;

中心化的交易中介會增加交易成本;

中心化的交易中介會限制小額支付;

交易雙方的隱私得不到保護;

人為控制的信任中介不可靠;

2、比特幣需要解決問題，包括：

用密碼學構建全新的信任機制，替代人為信任機制;

直接保護賣家免於欺詐;

通過第三方擔保機制，間接保護買家權益;

不可逆的記錄所有交易，解決「雙花支付」;

3、解決方式為：

通過點對點網路上的時間戳服務器來為所有交易排序，確保交易不可逆;

通過公私鑰數字簽名，構建密碼學信任機制;

如果能夠證明誠實節點的算力大於有共同作惡企圖的攻擊者算力總和時，系統安全。

由此可見，比特幣解決的問題是：做到用戶間不可逆的點對點直接支付。

最後，來看比特幣白皮書的結論部分，內容如下：

我們在此提出了一種不需要信用中介的電子支付系統。我們首先討論了通常的電子貨幣的電子簽名原理，雖然這種系統為所有權提供了強有力的控制，但是不足以防止雙重支付。為了解決這個問題，我們提出了一種採用工作量證明機制的點對點網路來記錄交易的公開信息，只要誠實的節點能夠控制絕大多數的CPU計算能力，就能使得攻擊者事實上難以改變交易記錄。該網路的強健之處在於它結構上的簡潔性。節點之間的工作大部分是彼此獨立的，只需要很少的協同。每個節點都不需要明確自己的身份，由於交易信息的流動路徑並無任何要求，所以只需要盡其最大努力傳播即可。節點可以隨時離開網路，而想重新加入網路也非常容易，因為只需要補充接收離開期間的工作量證明鏈條即可。節點通過自己的CPU計算力進行投票，表決他們對有效區塊的確認，他們不斷延長有效的區塊鏈來表達自己的確認，並拒絕在無效的區塊之後延長區塊以表示拒絕。本框架包含了一個P2P電子貨幣系統所需要的全部規則和激勵措施。

在對比特幣網路的技術體系做了非常詳盡的描述，並且證明了只要防止51%攻擊就能有效保障網路安全之後。中本聰做了以上總結，在總結中，他明確說明：

比特幣是一種不需要信用中介的電子支付系統(A system for electronic transactions without relying on trust)

其次，他提到了比特幣的幾項最關鍵的技術，這些技術也構成了以後區塊鏈的核心技術與思想：

1、工作量證明;

2、只要防止51%攻擊就能維護網路的健康，即簡單多數好人原則;

3、通過CPU算力投票，獲取記帳獎勵(即比特幣)，同時系統內產生新的可流通使用的比特幣;

4、最長鏈原則;

5、彈性的點對點網路，節點自由進出;

通過以上解讀，我們可以明確：比特幣不是金融傳銷。相反，他有一套非常科學的算法機制以及不受人為控制的運行機制。

這套運行機制完全通過全球幾十萬台高性能電腦(礦機)來共同維持，成為一個不可能停擺、交易無法回滾的電子支付系統。

02

自治機制

2.1 挖礦機制

由於沒有中心化機構發行比特幣，也沒有機構為往來交易帳目做記帳工作，所以必須要設計一套機制，在沒有中心化的管理下，通過算法保持不斷運行。

中本聰將比特幣預先「埋在」比特幣區塊鏈上，不被任何人所擁有。所有的節點(礦機)通過算力比拼競爭記帳權，競爭記帳權的方法是：哈希猜謎。

什麼是哈希猜謎呢?

有一種特殊的哈希值，前面會出現N個零，由於哈希算法具有不可逆性，所以只能通過不斷的正向加密嘗試，才能「猜到」前面會出現N個零哈希值的明文。零的數量越多，需要不斷試驗的次數越多，也就是難度越大。

算力就是在一秒內能計算這種加密算法的次數。算力越高，猜中的概率越高，拿到記帳權的概率也就越高，得到的比特幣獎勵也就越多。

比特幣網路上靠算力比拼，爭奪記帳權，一旦搶到了某個區塊的記帳權，就能夠得到比特幣獎勵。這就是比特幣的POW共識機制，又稱「工作量證明」。

獲得比特幣獎勵的過程稱為「挖礦」，購買用於挖礦的專用電腦設備稱為「礦機」，通過算力比拼獲取比特幣的人稱為「礦工」。

每隔10分鐘左右，比特幣網路上會產生一個新的區塊。區塊中打包了過去10分鐘內全網的所有交易記錄(嚴格講一個區塊中的交易記錄會受區塊鏈大小限制)，負責為這個新區塊記帳的礦工將獲取或者共同分享12.5個比特幣的獎勵。按今天的價格(美元3800/BTC)，也就是每隔10分鐘，將新增約47500美元的流動性，每天新增流動性近700萬美元。每隔四年，這個出塊獎勵會減半，也就是每天新增的流動性會減半。下一次減半大概在2020年5-6月之間某一天。

2.2 比特幣挖礦公式

根據比特幣源碼中的算法，我推算出以下比特幣挖礦公式，即一台算力為H的礦機，一天24小時內不間斷工作，能挖多少個比特幣：

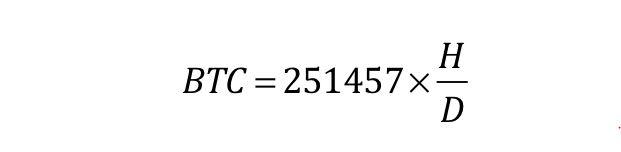
其中H是礦工擁有礦機的算力，D是當前難度。

**公式的推導過程見最後。

以S9礦機為例，一台的算力H=14500G，寫此文時的挖礦難度為：5,646,403,851,534

因此，24小時挖礦後，可以得到：0.000645743131個比特幣，按$4000元一枚的價格計算，每天約有$2.583的毛收入。

當然，礦機的運行需要電，於是我們有了下面的挖礦淨利潤公式：

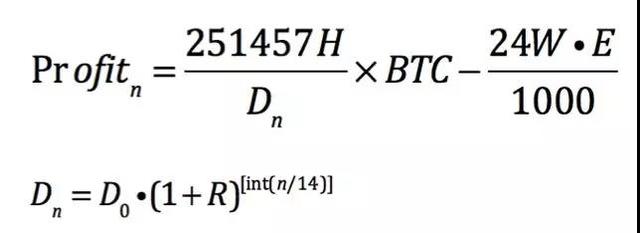
2.3 難度增長

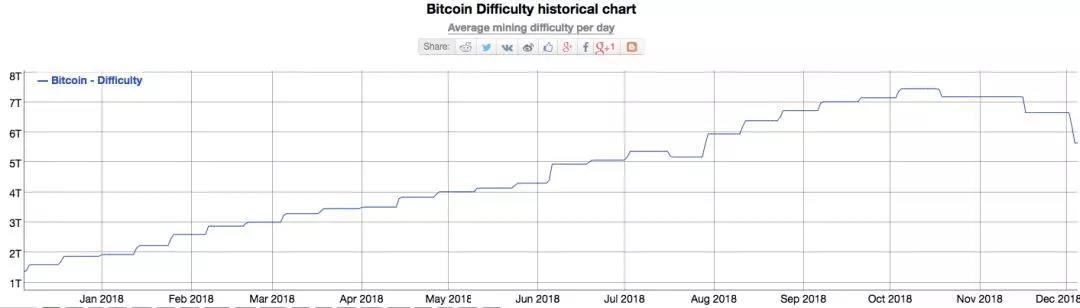
這里有一個非常重要的概念是：難度D會不斷增長，一般每14天增長一次。所以對於一台算力固定的礦機，他的收益是逐步下降的。

下圖是最近一年內的難度變化圖，可以訪問網址：https://bitinfocharts.com/comparison/bitcoin-difficulty.html 獲取即時的難度數據。

2.4 挖礦盈虧平衡

因為難度的不斷增長(最近因為BCH分叉，導致下降)，但是電費等支出是固定的，如果假設價格一定，每台礦機總有一天的產出不夠當天的電費等支出。於是我們可以計算出一台礦機能否回本，以及回本時間。

以目前主流礦機S9為例，該礦機的參數如下：

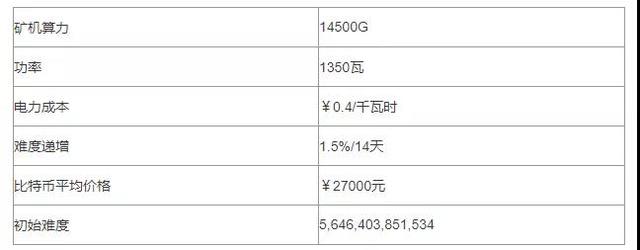
我們可以得到以下淨利潤圖形：

其中橫軸是天數，縱軸是累計淨利潤。

​

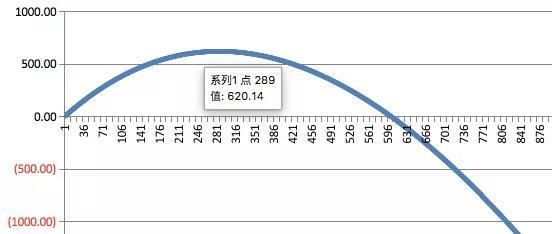
根據上圖，我們看到該台設備在289天的時候，最多能收回￥620元，如果過了這個時間點再挖的話，挖到比特幣的收益將低於電費支出，曲線開始下降。

￥620元這個價格就是該設備當前的合理價格，也是盈虧平衡點下的設備投資成本。

2.5 自治機制

通過上面公式以及計算，可以看出，當礦工的礦機算力增加時，獲得的比特幣數量也增加;而當隨著大量礦機加入挖礦，也會推動全網難度(D)的提升，難度的提升，又會降低單個礦工挖礦的收益。相反，如果難度(D)降低，則會提高挖礦的收益。這就是比特幣自適應機制的精華。

在這個自適應機制下，我們就能理解：為什麼比特幣價格會被不斷推高，為什麼比特幣在各種風波中仍能生存至今?

首先，隨著技術的進步，高算力礦機進入挖礦，試圖獲取比平均算力更高的算力優勢，以獲取更多收益。但這些新進入的礦機會迅速把總算力拉升，難度隨之飆升，不久，行業內會發現，挖礦並不划算。老的礦機退出，難度增長恢復到正常水平，挖礦的收益又提高了，於是，新的礦機又開始蜂擁而入。

如此反復，比特幣的價格就在礦工的一波一波自適應過程中上漲。每次因為外界原因，導致價格暴跌後，都會讓很多礦工離場，然後算力和難度下降，等挖礦成本降到與跌下來的價格相平衡的位置時，新的礦機又再一次進入。

比特幣就是在這種自適應機制下，從2009年年初一直動態的的運行至今。

以上兩部分介紹了比特幣的原理和算法，下篇會基於這些基本原理來分析支持比特幣上漲的理由以及可能導致比特幣歸零的風險。

我們下回見!

—-

**附：比特幣挖礦公式推導過程

Sha-256哈希算法會產生一個256位的二進制數，因此每次「猜謎」的成功概率為【2的256次方-1】分之一，也就是平均需要計算2的256次方 – 1次才能算出。

即：2**256 – 1 = 115792089237316195423570985008687907853269984665640564039457584007913129639935

當難度為D時，需要計算如下次數。(在Python中，**符號代表冪運算)

(0xffff * 2**208)/D

因此總的哈希次數為

D * 2**256 / (0xffff * 2**208)

因為每10分鐘產生一個區塊，10分鐘等於600秒，所以將上面換算成每秒算力：

D * 2**48 / 0xffff / 600

換算成10進制就是：

D * 2**32 / 600

筆者在推導本公式時是2017年8月15日，那天的難度D為：923,233,068,448。

帶入上述公式，在該難度下，需要算力：6,608,759,725,949,815,794，即6609P/秒的算力，才能在10分鐘內產生1個區塊，即12.5個BTC。

也就是需要：6609P / 12.5BTC = 528.72P 的算力才能挖出一個比特幣。

S9礦機13.5T/s算力，也就是528720T / 13.5T/s = 39164台機器挖礦，能在10分鐘內產生一個BTC。

也就是 39164 / 144個10分鐘 = 272台S9礦機，每天能挖一個BTC。

將以上過程整理成公式，設D為難度，H為算力(G為單位)，每天能挖的比特幣數量為：

600 * 10**9 * 12.5 * 144 * H / 2 ** 32 / D

將以上公式簡化為：

251457 * H / D

推導完畢。

以上推導嚴格按照比特幣源碼，實際操作中，時間上會有所延長或縮短，會對公式產生一些的影響，但總體上將保持一致。

筆者：博亞財經（WX:fun56778）