尋夢新聞LINE@每日推播熱門推薦文章,趣聞不漏接
商業數據分析的根本目的就是要洞察數據背後的規律,基於此,企業可以制訂決策、並採取相應措施和行動,進而達成想要的結果。這是商業數據分析的最大價值所在。
那麼如何才能洞察數據背後的規律,以給企業的決策提供支撐呢?
著名的咨詢公司Gartner於2013年總結、歸納、提煉出一套數據分析的框架,個人認為可以很好地回答上述問題,特此分享給大家。
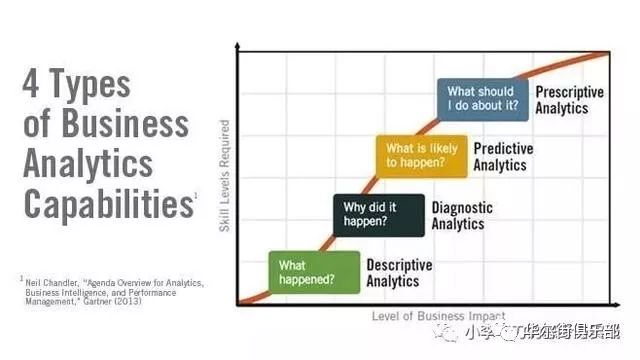
如上圖所示,Gartner把數據分析分為四個層次,分別是:
- 描述性分析(Deive Analysis)
- 診斷性分析(Diagnostic Analysis)
- 預測性分析(Predictive Analysis)
- 處方性分析(Preive Analysis)
描述性分析——發生了什麼?
故名思義,該層次主要是對已經發生的事實用數據做出準確的描述。比如某企業本月訂單簽約額比上月增加100萬,至1100萬,但是訂單履約率從上月的98%下降到了95%,庫存周轉率從上月的0.8下降到了0.7。
診斷性分析——為什麼會發生?
知道到底發生了什麼,對我們的幫助不大,更重要的是,我們要明白為什麼發生。比如經過分析,發現上文提到的訂單履約率下降的原因是成品生產不出來,無法完成交付。而成品生成不出來的原因則是部分原材料的供應商未能按時送貨,導致原材料不齊套,無法開始生產。
預測性分析——什麼可能會發生?
基於上述兩個層次的分析,我們發現了其中的規律,即原材料供應商的送貨及時率會影響成品訂單的履約率。假如上月某原材料供應商A送貨及時率只有70%,通過建模,我們可以預測本月該供應商會使我們的訂單履約率下降2%。
處方性分析——該做些什麼?
有了預測性分析的結果後,我們無需再做事後諸葛亮,而可以運籌帷幄,在事前就採取措施。上例中,供應商A會導致本月我們的訂單履約率下降,我們可能採取的措施就是把A換掉,但是現在有B和C兩個供應商供我們選擇,該選擇哪個呢?通過分析和計算得出:選用供應商B會比選C的訂單履約率高1%,因此建議選擇供應商B。這就是處方性分析。
四個層次層層遞進,經過這四個層次的分析以後,可以對企業的決策和行動提供有力支撐。接下來具體講講,這4種分析對應的商業分析場景。
描述性分析
描述性分析做為商業數據分析的第一個層次,主要回答『發生了什麼』的問題,接下來將對如何通過數據發現、描述和回答『發生了什麼』的方法和工具進行介紹。
一、方法
1、了解業務場景
如果想通過數據發現和回答『發生了什麼』的問題,第一步並不是急急忙忙的直接去分析數據,而是首先要了解和還原數據產生的業務場景,包括:數據涉及到的部門和崗位有哪些,這些部門和崗位之間的業務流程是怎麼樣的,在不同業務流程中有哪些輸入,對數據做了什麼處理,又是如何輸出和傳遞給下遊部門的。如果不了解業務場景就去做數據分析,就如同盲人摸象,因此這一步至關重要。
2、 探索性分析
探索性分析又細分為以下三個步驟:
① 提問,理順初步分析思路和目標
在了解清楚數據產生的業務場景後,可試著問自己一些what happened的問題。比如,本月銷售額是多少?環比和同比變化分別是多少?本財年銷售的變化趨勢是怎麼樣的?通過相應問題,可以理順初步的分析思路和分析目標。另外,在上一步了解業務背景的時候,也要注意和相關業務的關鍵幹系人溝通,獲取他們想知道的what happened的問題有哪些。
需要注意的是,這里說的是初步的分析思路和目標,因為在隨後做分析的時候,新的靈感可能會被不斷激發,分析的思路和目標也在不斷調整,這是一個循環往復的過程。
② 收集數據
有了初步的分析思路和目標以後,就可以確定需要收集哪些數據了。比如上文提到的銷售額分析可能用到的數據為銷售訂單數據、銷售開票數據。
③ 選擇相應分析方法
根據分析的思路和目標,就可以對收集到的數據選擇相應的分析方法了。具體的方法包括:
- 對數據位置的探索,包括:最大值、最小值、均值、中位數、分位數等
- 對數據分布的探索,包括:偏差、方差、標準差、莖葉圖、直方圖、箱形圖(也叫盒須圖)、密度圖等
- 對數據趨勢的探索,包括:同比、環比、趨勢圖、條形圖等
- 對數據聚合的探索,包括:排序、篩選、計數、重復項、分組、求和、比例、條形圖、餅圖等
3、提煉指標
對數據做探索性分析後,可對數據反映的事實有一個直觀的感受,比如,通過分析一個倉庫的月度收發存數據,可以大概知道這個倉庫的貨物周轉情況。但是要想更準確、簡潔地描述發生了什麼,還應該提出更高的要求:即總結和提煉出相應指標。比如描述庫存周轉的整體情況,庫存周轉率、庫存周轉天數等指標更有效。這些指標可以做為企業日常經營管理的KPI,讓相關人員快速、準確地了解到企業當前的經營情況。
二、工具
1、個人使用
描述性分析中最常用的工具就是Excel,但是隨著商業環境中產生數據的增多,Excel的運行效率變得相對低下,並且Excel主要側重於表格中的數字分析,但是因為人類對圖形的敏感度和理解力天生就比數字高,正所謂一圖勝千言,因此近年來可視化分析工具逐漸流行起來,此類工具主要是通過圖形去對數據產生洞見,發現其中的規律,而不僅僅是用做結果的展示。
FineBI就是其中之一。其上手比較容易,很多功能設計的也比較便捷和人性化,運行效率較高(10萬行以上的數據FineBI較Excel有明顯優勢),輸出的可視化圖表也很美觀,可直接用在數據分析報告dashboard里(Excel默認輸出的圖表都很醜,後期還需要做不少調整和美化,才能放到數據分析報告里)。
2、企業使用
對企業來說,描述性分析的工具主要是報表和BI。
報表一般是嵌入至各專業系統中,如CRM、SRM、ERP、WMS、MES等。
BI一般是單獨的系統,其從各專業系統中抽取數據,經過處理後,通過表格或圖形展示出來。過去Oracle的BIEE,IBM的Cognos,SAP的BO曾經在企業數據化建設上一度受歡迎,太猶豫這些工具過去龐大且上手難度大,在企業業務部門難以推廣。後來出現了新一代的自助式BI,目前最受歡迎的有Tableau、Qlikview,PowerBI,國內還有一家帆軟(沒錯就是我們)也被寫入Gartner報表市場推薦指南。這類自助式BI之所以受歡迎是,商業智能分析平台市場的主流已經從IT部門主導的靜態展示分析轉向業務部門主導的動態探索分析,這樣才能激發員工的主動性和創造力。
報表目前最受歡迎的是帆軟的FineReport,能製作各種複雜報表、以及數據可視化大屏。在報表和BI的基礎之上,可增加預警系統,如對異常的指標進行郵件或微信預警,讓主管僅對這些指標進行關注,而無需把所有的指標都看一遍,以節省時間,提高效率,有必要時再查看相應報表或BI展示,這也是企業描述性分析的應用方式之一。
關於描述性分析的方法和工具,涉及到的知識主要是統計學的內容,這部分知識需要大家自行找相關書籍進行補充閱讀。
診斷性分析&預測性分析
明確為什麼發生以及未來會發生什麼,這就是診斷性分析(Diagnostic Analysis)和預測性分析(Predictive Analysis)的作用。如何對問題做這樣的分析:
1、尋找相關特徵(feature)
在診斷性分析中,首先需要知道和結果可能相關的因素(在數據分析里,這些因素被稱為特徵)有哪些,這個過程一方面依賴於我們對業務的了解程度,另外也要多和業務人員進行頭腦風暴,只要是可能相關的,都納入考慮,也可以基於現有特徵構造新特徵,至於是否相關可在後面的分析中進行驗證。
比如和汽車油耗可能相關的特徵包括:車重、排量、軸距、變速箱類型(手動、自動)、驅動方式(兩驅、四驅)等。
2、相關性分析(Correlation Analysis)
列出和結果可能相關的特徵後,下一步就是要驗證這些特徵和結果到底是否相關。具體方法包括:
2.1 定性分析
2.1.1 二維散點圖
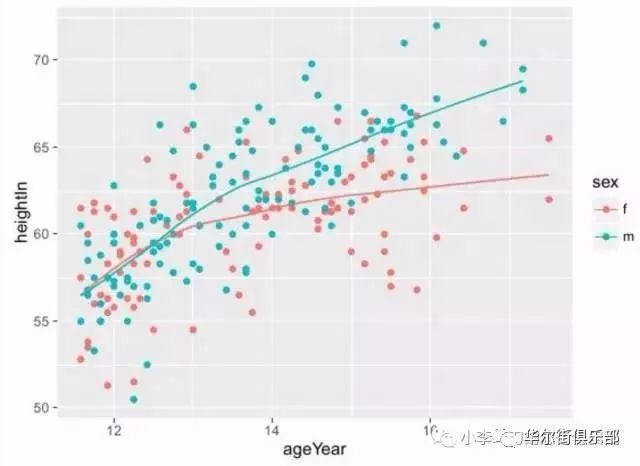
若分析的僅是一個特徵與結果的相關性,則可以通過畫二者的二維散點圖進行分析,通過圖形描述,可以初步且直觀判斷二者的存在何種相關關係:正相關、負相關、無關;如果相關的話,是線性相關還是非線性相關(拋物線、指數等)。下圖為不同性別年齡與身高關係的散點圖,可以看出在青少年時期,這二者是呈線性正相關的。
2.1.2 矩陣散點圖
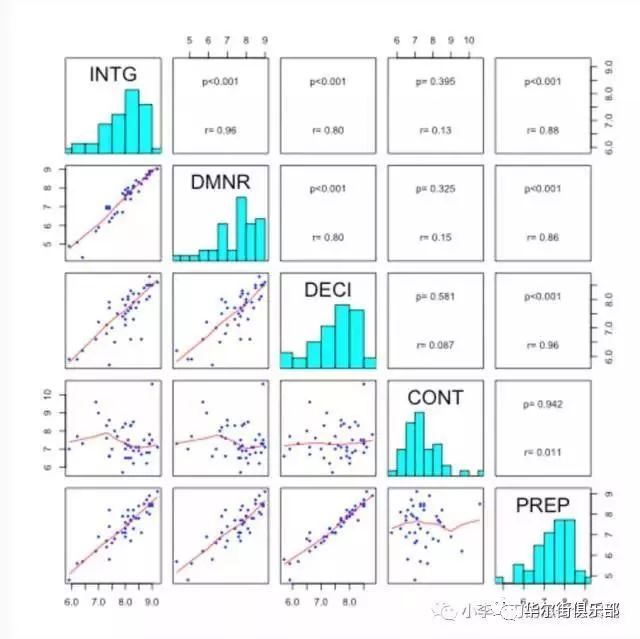
在現實中,僅有一個特徵與結果相關的情況是少之又少的,大部分情況都是存在多個與結果相關的特徵,此時需要矩陣散點圖進行分析。矩陣散點圖樣式如下:
其實質就是針對每一個特徵與結果分別做二維散點圖,以分析其相關性。當然,在矩陣散點圖上也可分析特徵與特徵之間是否有相關性,專業上稱呼為多重共線性,多元線性回歸要求模型中的特徵數據不能存在有多重共線性,否則模型的可信度將大打折扣,此時需要排除部分特徵消除共線性才能建模。
2.2 定量分析
上述的散點圖分析僅能通過圖形看出特徵與結果的大致關係,即定性分析;但是無法對它們的關係做精確性描述,即定量分析;定量分析主要分為如下兩個步驟:
2.2.1 特徵選擇
當我們列出可能和結果有關的多個特徵,並通過散點圖獲得大致的直觀認知後,還需要更精確的判斷到底哪個特徵與結果的相關性更高,為了降低計算的複雜度,我們應該只把那些最相關或者最重要的特徵放到模型中,主要的方法有兩種:
單變量特徵選擇方法:常用的手段有計算皮爾遜系數(即相關係數)和互信息系數,相關係數只能衡量線性相關性而互信息系數能夠很好地度量各種相關性,但是計算相對複雜一些,不過很多toolkit里邊都包含了這個工具(如sklearn的MINE),得到相關性之後就可以排序選擇特徵了;
基於模型的特徵選擇方法:部分模型本身在訓練過程中就會對特徵進行排序,如邏輯回歸、決策權、隨機森林等;
特徵選擇不僅有助於簡化計算,還可以幫助我們對特徵與結果的關係有更好的理解。
2.2.2 模型建立
2.2.2.1 回歸(Regression)
若結果為連續值,則應用的模型為回歸模型,包括:
一元線性回歸(Linear Regression)
若僅有一個特徵與結果相關,並且其是呈線性關係的,則可以進行一元線性回歸,即建立回歸模型y=a+bx計算出截距a和斜率b,x為特徵(自變量),y為結果(因變量);
多元線性回歸
上文中已經提到,在現實生活中,僅單個特徵與結果相關的情況是不多見的,大多數都是多特徵共同作用導致的結果。若通過矩陣散點圖判斷,各特徵無多重共線性,且與結果呈線性關係,則可以進行多元線性回歸分析,建立回歸模型y=a+b1x1+b2x2+…+bnxn;
非線性回歸(Non-Linear Regression)
如果回歸模型的因變量是自變量的一次以上函數形式,回歸規律在圖形上表現為形態各異的各種曲線,稱為非線性回歸。常見的非線性回歸模型包括:雙曲線模型、冪函數模型、指數函數模型、對數函數模型、多項式模型等;
那麼如何獲得上述的回歸模型呢?常用的回歸算法包括:最小二乘法、支持向量機(SVM)、GBRT、神經網路等。
2.2.2.1 分類(Classification)
若結果為離散值,則應用的模型為分類模型。比如人的年收入、日平均運動時間、日平均睡眠時間與人的壽命的相關關係是回歸模型;而人的年收入、日平均運動時間、日平均睡眠時間與人健康與否(健康或者不健康)的相關關係則是分類模型。
常用的分類算法包括:決策樹、邏輯回歸、隨機森林、樸素貝葉斯等。
2.2.3 監督式學習(Supervised Learning)
上述回歸模型和分類模型均是機器學習的監督式學習模型,它主要指通過學習歷史的真實數據,找到其中的規律(即模型),並假設「歷史總是驚人的相似」「太陽底下沒有新鮮事」,通過找到的模型對未來進行預測。這一種學習方式相當於既包括了診斷性分析,也包括了預測性分析。但是,通過歷史數據找到真正的規律是比較難的。在現實生活中大家應該都有這種感覺,回顧過去好像清清楚楚,但是展望未來時又是一片迷茫。這是因為實踐和未來才是檢驗規律的唯一標準,但是在未來還沒有發生的情況下,檢驗只能依靠歷史的數據,這樣非常容易出現機器學習中常說的過擬合和欠擬合的問題。如何評估機器學習模型的效果,避免過擬合和欠擬合的問題,找到那個真正的規律,業界提出了很多的方法,限於篇幅的原因,只能在其他文章中下回分解了。
3. 因果性分析
診斷性分析的隱含意思就是,要找到事物的因果關係,即因果性分析。所謂因果性,假設X是因,Y是果,則只要X出現,必然會導致Y的發生,其是百分之百的概率。
雖然我們在上文中介紹了相關性分析,但是需要特別注意的是,相關性分析並不等同於因果性分析,相關性分析可達不到百分之百的概率。比如,雖然收入與個人的健康有很大的關係,因為收入高的人可以享受更好的物質和醫療,但是並不意味著有錢人就一定健康,現在有錢人英年早逝的新聞經常見諸報端,因此我們只能說收入與健康是呈相關性,而非因果性。
但是,在現實世界中,很多事務的因果性是很難被證實的,因為其追求的是百分之百的概率,一點差錯、一個反例都不能出。「吸煙有害健康」這句話聽了很多年,現在聽起來好像這兩者之間存在因果性,但是其實它們也是相關性,只不過是強相關性。因為要證明所有吸煙的人健康都受到了影響,這件事是很難的。
所以,回過頭來,做診斷性分析時,我們依然要從相關性分析出發,並結合相關領域的知識,通過邏輯推理,對分析的結果進行合理解釋。因此,在使用機器學習的模型時,也要注意其可解釋性。
另外,在大數據時代,我們看問題和分析問題時,也要轉換自己的思路,從以往的尋找確定的因果性改為尋找強相關性。
處方式分析
處方式分析回答的問題是:為了解決這個問題,我們該做些什麼?或者說,為了達到某個目標,我們該朝哪個方向努力?
那麼如何通過處方式分析給出相應問題的解決方案和行動建議呢?
首先,還是要進行描述性分析。通過描述性分析明確現狀和問題,及業務人員和管理人員的需求,這樣才能做到有的放矢。
其次,進行診斷性分析,尋找和當前問題相關的特徵,並對其進行建模。
上述兩個步驟在前面的文章中已經做了詳細介紹。
最後,根據不同的業務場景和需求,給出具體的解決方案和行動建議。具體方法又分為以下三種:
1. 預測性分析
有一些情況,僅僅使用診斷性分析和預測性分析的模型,即可以給出建議,比如銀行可根據申請人的基本信息,包括學歷、收入、是否有車、是否有住房、存款金額、是否有違約記錄等,去建立模型預測其信用違約的風險有多大,進而給出建議是否要給這個申請人發放信用卡,如果要發放,信用卡的額度又該是多少。
2. 仿真(Simulation)
仿真就是通過建模模擬真實世界的系統或流程,並通過不同的輸入參數或條件查看其對結果的影響,據此制訂相應決策。仿真在各行各業已經有廣泛的應用,比如軍事上初級的沙盤推演、中級的電腦模擬對抗、高級的實戰演習,都是仿真。再比如飛機設計時初級的軟件CFD(計算流體力學)仿真、中級的風洞實驗、高級的試飛,也是仿真。當然,越高級的仿真付出的成本就越高,所以在商業環境中,主要是通過在電腦上做數學建模仿真,進而根據仿真結果給出相應的解決方案和行動建議。比如企業的成本支出和客戶服務水平是一個兩難問題,往往成本的削減意味著客戶服務水平的下降,那如果說企業要制訂年度成本削減目標,通過仿真發現成本降低5%,但是客戶服務水平僅下降1%,屬於可接受範圍,但是當成本降低10%時,客戶服務水平下降達6%,可能對公司的經營、商譽等產生重大影響,則此時成本降低5%是相對合適的,而10%就不是那麼合適了。
3. 最優化( Optimization)
最優化是應用數學的一個分支,主要指在一定限制條件下,選取某種研究方案使目標達到最優的一種方法。最優化問題在當今的軍事、工程、管理、商業等領域有著極其廣泛的應用。比如,企業都希望利潤盡量高,那如何在現實的約束條件下,達到上述目標就是一個普遍的最優化問題。最優化常用的方法為線性規劃、非線性規劃、凸優化、整數規劃、網路流優化(物流、電網、通訊網路應用)等。
處方式分析是數據分析方法的最高階形態,也是在商業環境中對企業最有用、產生價值最大的方法,因此希望大家未來不管是在做數據分析時,還是在設計數據產品時,都能以此為目標,我們一起共勉。
來源:轉自帆軟軟件的今日頭條號 作者 李應龍 8年供應鏈管理相關工作經驗,現在杭州一家通過機器學習和數據分析的方法,解決企業供應鏈問題的創業公司負責產品設計的工作 由中國投行俱樂部綜合整理,轉載請註明來源
免責聲明:所載內容來源互聯網,微信公眾號等公開管道,我們對文中觀點保持中立,僅供參考,交流之目的。轉載的稿件版權歸原作者和機構所有,如有侵權,請聯繫我們刪除。