​​撰文 | 丁玖（南密西西比大學數學教授）

紀念”信息論之父”香農的最好方式，莫過於重溫一下他怎樣定義信息熵的數學思想，去理解現代信息論這個基本概念——僅用初等代數即可推導，令人賞心悅目，流連忘返！

確定性過程在數學里是司空見慣的現象。眾所周知，一個函數的迭代過程是確定性的，因為下一個迭代點完全由當前已知的迭代點唯一地確定。譬如混沌學中著名的邏輯斯蒂模型 f(x) = 4x(1-x) ，當x等於0.1時的函數值必為0.36，而不會等於0.35或0.37。同樣，一個微分方程初值問題的解也是確定性的：解在任一時刻的值是唯一確定的一個數。

然而，和確定性現象一樣, 隨機現象在自然界也是到處可見的。小孩子們喜歡猜硬幣正反面的遊戲：將一枚五分錢的平整硬幣在桌上旋轉，然後猛地用手把它拍倒按住，猜猜是錢的正面朝上還是反面朝上。即便旋轉過一百次都是正面朝上，第一百零一次旋轉後，硬幣正面朝上的或然率還是同一個概率值：1/2。這就是典型的隨機性，它意味著試驗結果是不可確定的。如果歷史上英國鑄幣局（牛頓（1643-1727）曾在這里當了幾十年的局長）把錢幣故意制成一個圓錐體陀螺形狀，那麼無論怎樣旋轉，待它最終停轉時總是站在那里，也就是說正面總是朝上，這就是一個確定性的例子——旋轉結果是可以預測的。人們認識到隨機性的歷史也許比數學史本身還要長，甚至可能就等於人類自己的歷史——畢竟，孕婦肚子里懷的是兒子還是女兒，本身就是一個不可預測的隨機事件問題。

不確定性作為自然的基本屬性，應該怎樣用數學的語言去刻畫呢？「熵」就是關於不確定性的一個極好的數學描述。歷史上的熵概念起源於熱力學。凡是學過熱力學、統計物理或物理化學的人對「熵」這一術語都不陌生，但是這一概念發展的初始階段卻跟混沌思想並無任何歷史瓜葛。實際上，當熵的名詞誕生之時，混沌之祖龐加萊（Henri Poincare, 1854-1912）還只是一個乳臭未乾的少年。當熵的觸角從宏觀的熱力學伸展到微觀的統計力學之後，才逐漸拉近它和混沌概念的距離。二十世紀中葉的一場信息論革命，無意中在古典熵的舊作坊內又釀造出醇香的新酒。

十九世紀是物理學家大顯身手的世紀。如果說十七世紀是宏觀力學的樂園，十九世紀則是微觀力學的會所。熱力學和統計力學把眼光由外向里地從機械能轉向到內能，熵概念的緩慢演化覆蓋了那個世紀後半葉的前三十年。1865年，熱力學奠基人之一、德國物理學家和數學家魯道夫 • 克勞修斯（Rudolf Julius Emanuel Clausius, 1822-1888）第一次使用了「熵（entropy） 」 （從意指「變換容度」的希臘詞τροπή派生而來）作為熱力學的專用名詞，並賦予其數學形式。他用 「Sadi」 的第一個大寫字母 S 作為熵的記號，大概是為了紀念熵理論先驅者之一、法國工程師薩迪 • 卡諾（Nicholas Leonard Sadi Carnot, 1796-1832）。他寫道：「按照希臘詞τροπή (trope) 的意思，我將 S 這個量稱為系統的熵。我特別取熵這個詞是為了讓它與能量這個詞盡可能相像：這兩個詞所表達的兩個量在物理上如此密切相關，把它們的名字寫得類似完全是合情合理的。」 他的一句名言 「宇宙之熵趨於無窮」 是熱力學第二定律在孤立系統中無能量消耗情形下的推論；他的另一句斷言 「宇宙總能量不變」 則是能量守恒定律的通俗說法。

第二年，24歲的玻爾茲曼（Ludwig Boltzmann, 1844-1906）在他關於氣體動力學的奠基性論文中，給出了熵的另一形式。十一年後的1877年，他在統計熱力學中把熵簡單地定義為著名的「玻爾茲曼常數」乘上與宏觀狀態相容的微觀狀態的個數之對數。與早先把熵和熱量傳遞捆綁在一起的做法不盡相同，玻爾茲曼把熵看成是無序分子運動紊亂程度的一種度量。這種新觀點，被楊振寧先生（1922-）十分推崇的美國物理學家、化學家和數學家威拉德 • 吉布斯（Josiah Willard Gibbs, 1839-1903）精雕細琢，成為統計力學理論發展史上的里程碑之一。1995年夏，在中國廈門大學召開的第十九屆國際統計物理大會（東道主學者郝柏林（1934-2018）時任會議主席）上，筆者曾聽到與會講話的楊振寧先生建議大家讀讀二十世紀初吉布斯那本啟迪靈感的名著《統計力學的基本原理》（Elementary Principles in Statistical Physics, 1902）。吉布斯於1863年在耶魯大學獲得美國歷史上第一個工程博士學位，並在這所老牌大學度過了他的整個學術生涯。他令蒸蒸日上的美國揚名天下，可惜牆內開花牆外香，在科學整體尚欠發達的祖國，吉布斯活著的時候聲名未曾顯赫，卻在去世前兩年被大西洋彼岸最強盛時期的英國授予了倫敦皇家學會的考普利獎（Copley Medal of the Royal Society of London）——諾貝爾獎之前全世界科學界名氣最大的獎項。

1. 信息熵

對需要交流的人類而言，通訊猶如吃飯睡覺一樣重要。就像人類不斷探索水稻增產一樣，不斷改進通訊質量與速度的科學研究一直是全世界方興未艾的事業。1948年，博士畢業後就在貝爾實驗室里研究通訊技術的電子工程師克勞德 • 香農（Claude Shannon, 1916-2001）在《貝爾系統技術雜誌》（Bell System Technology Journal）上分兩期發表了他一生中也許是最有名的一篇論文：《通訊的數學理論》（A mathematical theory of communications,1948），引入了一條全新的思路，震撼了整個科學技術界，開啟了現代信息論研究的先河。在這一偉大的貢獻中，他引進的「信息熵」之一般概念舉足輕重：它在數學上量化了通訊過程中「信息漏失」的統計本質，具有劃時代的意義。

克勞德 • 香農（Claude Shannon, 1916-2001）

香農生於美國密歇根州，本科畢業於「美國大學之母」密歇根大學。他兒時崇拜的英雄人物是大名鼎鼎的、造福全人類的美國大發明家托馬斯 • 愛迪生（Thomas Alva Edison, 1847-1931），後來他發現這位英雄是他家的一個遠親。二十歲本科畢業時，他拿回了電子工程和數學兩張學士文憑。而他在密西根大學修課時接觸到英國數學家和哲學家喬治 • 布爾（George Boole, 1815-1864）最有名的工作「布爾代數」，成就了他二十一歲在麻省理工學院完成的題為《中繼及開關電路的符號分析》（Symbolic analysis of relay and switching circuits，1937）的碩士學位論文。有人說這是二十世紀甚至人類歷史上最有價值的碩士論文，因為它用布爾代數的理論首次表明對付真假李逵的「符號邏輯」與對付電路開關的「0-1數字」具有一致性，從而論證了數字計算機和數字線路的邏輯設計之可能性。

香農最初並沒有借用「熵」這個詞匯來表達他關於信息傳輸中的「不確定性」的度量化。他甚至都不太知曉他所考慮的量與古典熱力學熵之間的類似性。他想把它稱為「information（信息）」，但又認為這個名詞太過大眾化，已被普通老百姓的日常話語用濫了。他又考慮過就用單詞「uncertainty（不確定性）」，但它卻更像抽象名詞，缺乏量化的餘地，確實難於定奪。終於有一天，他遇見了天才的數學家馮 • 諾依曼（John von Neumann, 1903-1957）。真是找對了人！馮·諾依曼馬上告訴他：

就叫它熵吧，這有兩個好理由。一是你的不確定性函數已在統計物理中用到過，在那里它就叫熵。第二個理由更重要：沒人真正理解熵為何物，這就讓你在任何時候都可能進能退，立於不敗之地。

香農的信息熵本質上是對我們司空見慣的「不確定現象」的數學化度量。譬如說，如果天氣預報說「今天中午下雨的可能性是百分之九十」，我們就會不約而同想到出門帶傘；如果預報說「有百分之五十的可能性下雨」，我們就會猶豫是否帶傘，因為雨傘無用時確是累贅之物。顯然，第一則天氣預報中，下雨這件事的不確定性程度較小，而第二則關於下雨的不確定度就大多了。

對於一般的不確定事件，我們怎樣數學地刻畫它的不確定程度呢？設想有n個「基本事件」，各自出現的概率分別為

則它們構成一個樣本空間，可以簡記為所謂的「概率數組」

樣本空間最簡單的例子是我們上面提到的拋硬幣遊戲，它只有兩個基本事件：拋硬幣結果是「正面朝上」或「反面朝上」，其中每個事件的概率均為 1/2，其對應的樣本空間為 (1/2, 1/2)。如果鑄幣廠別出心裁地將硬幣做成兩面不對稱，使得拋硬幣時正面朝上的概率增加到7/10，而反面朝上的概率減少到3/10，則對應的樣本空間就是 (7/10, 3/10)。如果我們用符號 H(1/2, 1/2) 來表示第一個樣本空間的不確定度，用數 H(7/10, 3/10) 代表第二個樣本空間的不確定度，那麼直覺馬上告訴我們：數 H(1/2, 1/2) 大於數 H(7/10, 3/10)，也就是前者比後者更加不確定。

更一般地，若用

記樣本空間

所對應的不確定度，運用同樣的直覺分析，我們相信當所有的基本事件機會均等，即都有同樣的概率1/n時，其不確定度最大。因而，不確定度函數H應該滿足如下的基本不等式：對所有的加起來等於1的非負「概率數」

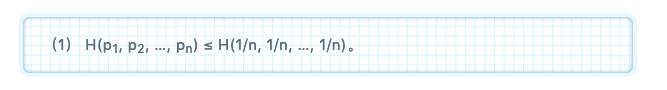
如果我們不拋硬幣，而像澳門賭場的常客那樣擲骰子，每擲一次，小立方骰子的每一個面朝上的概率均為1/6。想一想就知道，某個指定面朝上的不確定度應大於玩硬幣時正面或反面朝上的不確定度。將這個直觀發現一般化，我們就有不確定度函數H 應該滿足的單調性要求：

假設物理系趙教授、數學系錢教授和孫教授競爭理學院的一筆科研基金，他們每人申請成功的概率分別為1/2、1/3、1/6。院長為求公平，讓每個系得此獎勵的機會均等。若物理系拿到資助，就到了趙教授的名下。如數學系得到了它，錢教授有2/3的概率拿到，孫教授則有1/3的機會到手。通過分析「條件概率」，我們能得出不確定度 H(1/2, 1/3, 1/6) 的數值：這三個教授獲得基金的不確定度，等於物理系或數學系拿到這筆基金的不確定度，加上數學系贏得該基金的概率與在數學系拿到基金的條件之下，錢教授或孫教授得到它的不確定度之乘積。換言之，H(1/2, 1/3, 1/6) = H(1/2, 1/2) + ½ H(2/3, 1/3)。推而廣之，可以得出不確定度與條件概率有關的「加權和」性質：

既然我們想用一個漂亮的數學公式來表達不確定度這一樣本空間概率值函數，我們自然希望這個函數表達式和幾乎所有的物理公式一樣連續依賴於公式中的所有變元。這樣，第四個條件就自然而然地加在了不確定度函數的頭上：

香農無需什麼高深的數學，甚至連微積分都可不要，就證明了：任何在所有樣本空間上都有定義的函數H，只要它滿足以上的「三項基本原則 (2)(3)(4)」，就非如下的表達式莫屬：

其中符號 ln 代表以 e 為底的自然對數函數，C 可以是任意一個常數。並可證明，條件(1)自動滿足（有興趣的讀者可用初等微積分證之）。當然，熵公式的證明需要的是一種創造的頭腦思維、一手精湛的代數技巧、一個巧妙的極限思想。如果C取成玻爾茲曼常數，它就能和當年吉布斯在統計熱力學中得到的「吉布斯熵」一模一樣。香農取 C = 1，如此得到了非負函數：

按照馮 • 諾依曼的建議，該函數被定義為樣本空間 (p1, p2, …, pn) 所對應的信息熵。現在，這個數被廣稱為「香農熵」，以紀念它的創造者、信息論之父——香農。

現在，為了滿足讀者追根求源的好奇心，我們在此給出一個高中生也能看懂的簡單證明。這是活學活用初等代數的好機會，我們分三步來證明：

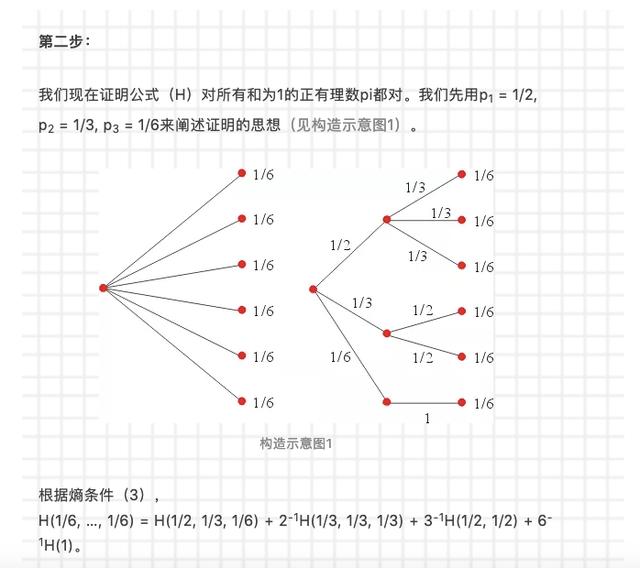
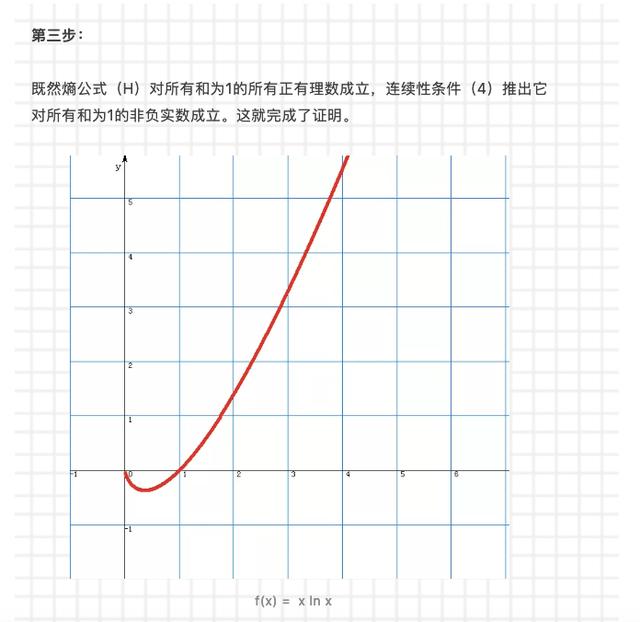
如上證明是我在1989年從我的博士導師李天巖教授於密歇根州立大學所作的公眾報告中聽到的。細看一下香農熵的公式，除了負號，它是基本函數 x ln x 的有限個函數值之和。這個函數的圖像就像大廚師手中側面看過去的長勺子。向上彎曲的曲線有幾何性質：連接上面任意兩點的直線段都在這兩點之間的曲線段之上。運用初等微分學，讀者可以證明，對任意兩個正數a和b，有

a – a ln a ≤ b – a ln b。

這就是現在冠以吉布斯大名的初等不等式，在一切與熵有關的數學問題中均有上乘表現，比如說我們在下面的第3節就要用到它。

當所有的概率值pi都取為1/n時，吉布斯熵就還原成玻爾茲曼熵，它可看成是最大可能的吉布斯熵。同理，這時的信息熵取值最大，等於 ln n。

2. 柯爾莫果洛夫熵

不到十年，香農熵就在離散動力系統的練武場上大展身手。這主要歸功於三十年代就建立了公理化概率論的俄羅斯數學巨人柯爾莫果洛夫（Andrey N. Kolmogorov, 1903-1987）和他在遍歷理論領域的最佳弟子西奈依（Yakov G. Sinai）。五十年代中期，柯爾莫果洛夫在考慮遍歷理論的「共軛不變量」這一基本問題時開創了「度量熵」的理論，而他的門徒西奈依的工作則使得它日臻完美。度量熵揭示了一般非線性函數迭代最終走向的動態性質，從而和稍遲一點發展的混沌理論融合了起來。

柯爾莫果洛夫（Andrey N. Kolmogorov, 1903-1987）

柯爾莫果洛夫堪稱俄羅斯民族二十世紀的龐加萊，在國際數學界備受尊崇。他的父親於沙皇時期投身革命，被聖彼得堡當局驅逐，最後消失在內戰之中。因母親在生產過程中不幸去世，他隨姨媽在富有的貴族外祖父的莊園中長大，並受到很好的早期教育。比馮 • 諾依曼大八個月的柯爾莫果洛夫一樣是一個歷史愛好者。十七歲進入莫斯科大學後，他參加了俄羅斯著名歷史教授的討論班，並寫出了他一生中的第一篇論文，研究內容不是數學，而是四個世紀前的俄國一個城市的發展史。他頗為得意地問教授，該文可否發表？出乎他意料的回答是：「肯定不行！你的論據只有一個，對歷史學而言太少了，起碼得有五個論據才行。」這位嚴謹的教授應該成為國內某些發表論文心切的人文科學工作者的大楷模。但也正是這位打擊學生信心的歷史教授在無意之中把柯爾莫果洛夫推向了另一個五六歲時就萌芽的至愛，並令他矢志不渝——因為在數學中定理只需一個證明就夠了！

幾乎在精心研究俄國歷史的同時，年紀輕輕的柯爾莫果洛夫證明了集合論以及三角級數的幾個結果。尤其是在1922年，他構造出一個幾乎處處不收斂的三角級數，一下子成了令人矚目的國際數學新星。在那一時刻，他立馬決定「把一切獻給數學」，他的決心就像兵工英雄吳運鐸《把一切獻給黨》一樣堅定。在半個世紀的數學生涯中，柯爾莫果洛夫大大推進了現代數學的許多分支領域的發展，如函數論、概率論、直覺主義數理邏輯、泛函分析、拓撲學、隨機過程、經典力學、紊流、遍歷理論、計算複雜性等等，被公認為二十世紀全人類最偉大的數學家之一。如果美國數學史家貝爾（ Eric Temple Bell, 1883-1960）晚生五十年，也許他那本大作《數學大師：叢芝諾到龐加萊》（Men of Mathematics, 1937）會以柯爾莫果洛夫作為壓軸戲，將他稱為「最後的全能數學家」，而龐加萊則變成歷史上「倒數第二個全能數學家」。

西方物理學界有偉大的導師費米帶出了一大批傑出的學生，甚至有好幾個得了諾貝爾獎，可是西方沒有哪個數學家會像柯爾莫果洛夫那樣培養或影響一個接一個的天才學生。上世紀六十年代初曾讓美國數學新星、1966年菲爾茲獎獲得者斯梅爾（Stephen Smale, 1930-）驚羨的「動力系統四大才子」中的阿諾德（Vladimir I. Arnold, 1937-2010）和西奈依便是他的弟子。除此之外，柯爾莫果洛夫成果最輝煌、名聲最響亮的學生是沒有上過高中和大學就直接成為其博士生的猶太人伊斯雷 • 蓋爾芳德（Israil Moiseevic Gelfand, 1913-2008）。在與其名Israil只有一個字母之差的猶太國度Israel（以色列) ，蓋爾芳德和「物理女王」吳健雄（1912-1997）一同站在了第一屆沃爾夫獎的領獎台上，甚至比他的老師還早了兩年獲此殊榮。按照華東師范大學數學系教授張奠宙 (1933-2019) 在其著作《二十世紀數學經緯》（2002）中所統計的，柯爾莫果洛夫直接指導過的學生有六十七人之多，可媲美孔子「賢弟子七十二」的記錄，其中有十四人被選為蘇聯科學院院士或通訊院士（具體名冊可見書本第368頁），堪稱中國孔聖人的強勁對手。

東方數學界里，在培養學生方面或許能和柯爾莫果洛夫有「最佳逼近」距離的是中國最偉大的數學家華羅庚（1910-1985）。他門下的數論學家陳景潤（1933-1996）證明了離哥德巴赫猜想最近的「1+2」情形，這一傳世工作讓二十世紀六七十年代的世界數學界再次對中國刮目相看。華羅庚的其他傑出弟子，如解析數論的王元（1930-）、多復變函數論的陸啟鏗（1927-2015）和龔升（1930-2010）、抽象代數學的萬哲先（1927-）等，都是在國際上頗有影響的純粹數學家。

讓我們再回到玩硬幣的遊戲，來經歷一次柯爾莫果洛夫開發度量熵的思想之旅。但是，這一次我們不只注意拋一次硬幣正面朝上或反面朝上的結果，而是一口氣拋上好幾次看看有多少種可能性發生。比如連續上拋兩次，就有四種可能結果出現：正正、正反、反正、反反。因為第一次拋硬幣結果對第二次結果毫無影響，它們是相互獨立的，因而四種結果的每一次可能性均為四分之一。

國外硬幣的正面通常是本國名人頭像，如美國放的就是歷史上最偉大的幾個總統。

一分硬幣（左）上面是亞伯拉罕 • 林肯（Abraham Lincoln, 1809-1865），五分硬幣（下）上面馬斯 • 傑弗遜（Thomas Jefferson, 1743-1826），一角硬幣（上）上面是弗蘭克 • 羅斯福（Franklin Delano Roosevelt, 1882-1945），一元硬幣（右）上面喬治 • 華盛頓（George Washington, 1732-1799）。

為簡化書寫，我們用英文字母H（Head，頭）代表正面朝上，T（Tail，尾）代表反面朝上，這樣兩次拋硬幣的所有可能性可以簡記成：HH, HT, TH, TT。更一般地，若連續地拋上n次硬幣，則有2n個可能結果，每一個結果的概率均為

​每一個結果都是一個基本事件，我們就有了一個包含2n個基本事件的樣本空間

其香農熵的值為 n ln 2。

我們的直覺是，無論拋了多少次，對下一次的結果我們仍然心中無數。作為一個極端例子，假如拋了一百萬次都是頭像朝上，第一百萬零一次呢？頭像朝上還是尾巴朝上？閣下打賭的勝率如何？柯爾莫果洛夫對下面的問題大感興趣：倘若已知連續拋了n次硬幣的結果，接下來拋第n+1次的結果的不確定度到底是什麼？

讓我們再來一點數學思維吧。數學家愛數字勝於愛符號。正如美國物理學家費恩曼（Richard Feynman, 1918-1988）生前所經常回憶到的，他那善於培養孩子好奇心的父親很早就告訴他：知道事物的名稱並不重要，重要的是知道其內容。熵在英文里叫entropy，在德文或法文里都是entropie，在俄文里是eнтропия。即便認得一百種語言的名詞「熵」，卻對它的意義知之甚少或一無所知，甚至不以為然，這只有孔乙己才可能做得到，或培養出孔乙己的私塾先生喜歡這樣做。可是目前我們學校的一些教育方式本質上就是在這麼做。

我們用數字0代替H，數字1代替T。然後連續n次拋硬幣的結果可用小數

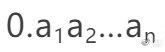
來代表，其中小數點後面的每個數字非0即1。而這個數實際上可看成是0和1之間的一個數x的「二進制表示」。我們的雙手有十個指頭，日常生活中，我們最喜歡十進制了，它是如此的方便，不懂算術者也可扳扳指頭計算。但是，如果一位學過計算機原理的人告訴我們11可以表示「周期三意味著混沌」中的那個數3，我們可能以為他是瞎說。不，他是對的，因為他用的是計算機中央處理器內運算所用的二進制！二進制最早在萊布尼茲（Gottfried Wilhelm Leibniz, 1646-1716）的著作中出現，他可稱為人類歷史上首位計算機科學家！十進制中，我們「逢十進一」，而在二進制中，就要「逢二進一」了。這樣，在二進制中，自然數從小到大排列的前幾個數是 1,10,11,100,101，它們分別是我們習以為常的十進制數 1,2,3,4,5。我們從小學的算術熟知，在十進制中小數0.31416可以被展開成「有限項級數」形式：

以此類推，在二進制中小數0.10011有展開式

這樣，每一個二進制小數 x = 0.a1a2…an 都可以寫成

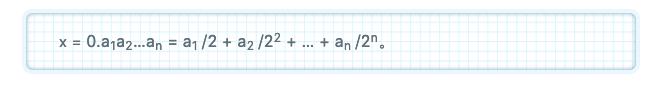
現在我們把區間 [0,1] 一分為二：左邊的半個區間 [0,1/2) 和右邊的半個區間 [1/2,1]。注意，為了敘述嚴格起見，這兩個子區間前一個是「左閉右開」的，後一個是「雙邊都閉」的，它們的交集為空集，亦即沒有共同的元素。顯而易見，若

則x屬於 [0,1/2)，若

1，則x位於 [1/2, 1] 之中。想想看

怎樣確定x的位置？

我們可以借用把 [0,1] 區間映到自身上的一個逐段線性的「加倍函數」來解釋連續拋硬幣的數學遊戲。這個函數的定義是：當x大於或等於0並且小於1/2時函數值為2乘上x，而當x大於或等於1/2並且小於或等於1時函數值為2乘上x再減去1。更簡單地說，這個函數就是將自變量加倍，再丟掉結果的整數部分。它的簡潔表達式就是 f(x) = 2x (mod 1)，其函數圖像是兩條斜率是2、彼此平行的斜線段。它是保持長度的，意思是任何子區間和它在 f 下的逆像都有相等的長度。一個區間在函數下的逆像是函數定義域中所有那些數的全體，這些數的函數值都落在該區間內，它可以通過函數圖像畫水平、垂直線得到。這個加倍函數不是處處連續的，在區間的中點1/2處有個躍度為1的跳躍性間斷，這從圖像上一眼就知。用更專業的術語講，它是一個「勒貝格可測函數」。加倍函數和邏輯斯蒂模型一樣，都是混沌學家教書時寵愛的混沌例子。

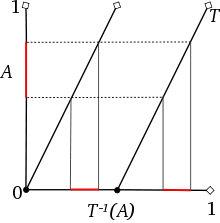
f(x) = 2x (mod 1)，x∈[0,1]

動力系統尋找的是過程的終極行為。當自然數n走向無窮大時，上述不確定度的極限值就被稱為函數 f 關於劃分 P 的熵。這個熵值依賴於函數定義域區間 [0,1] 的劃分。該定義域可以被劃分為任意有限多個彼此互不相交的子集之並，而不同的劃分一般給出不同的熵值。定義域的所有劃分所對應的熵的「最大值」（更嚴格地說，是對應於所有的有限劃分的熵值之「最小上界」，因為無窮個數放在一起可能找不到最大數，比如所有比3小的正數沒有最大值，但其最小上界為3）就叫做 f 的柯爾莫果洛夫熵，又稱為測度熵或度量熵，因為它用的是勒貝格所開創的一般測度論工具來度量保測函數迭代最終性態的混亂程度。

我們用來描繪硬幣遊戲的這個加倍函數的度量熵等於2的自然對數：ln 2 。請注意，這是一個正數。如今動力學家們都已知道，具有正熵的確是混沌動力系統的一個典型性質。同法可知，將自變量增加六倍後再丟掉結果整數部分的「六倍函數」（數學上這個函數可寫成 6x(mod 1)的形式，圖像是六根斜率為6的平行斜線，其不連續點為 1/6, 1/3, 1/2, 2/3, 5/6），它的測度熵則為 ln 6。六倍函數可以看成是擲六面骰子（有六種均等機會出現）結果之不確定度。「十倍函數」 10x(mod 1) 的熵是 ln 10，而「百倍函數」 100x(mod 1) 的熵則跳到 ln 100了，依次類推。倍數越提高，熵值越變大，不確定度就越可觀，這就是為何在無線通訊中，工程師們常用高度混沌的「高倍函數」參與信號的傳輸。

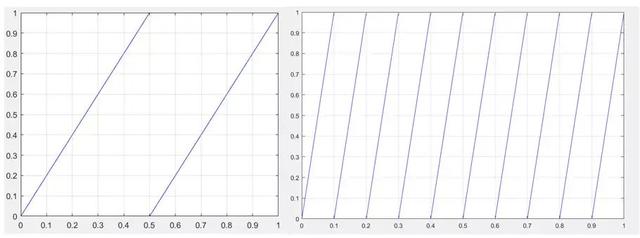
二倍函數f(x) = 2x(mod 1)（左）與十倍函數f(x) = 10x(mod 1)（右）的圖像對比。

柯爾莫果洛夫熵是遍歷理論中的一個極其有用的共軛不變量，即彼此共軛的保測函數共享同一熵值。事實上，早在1943年，人們就已經知道以概率論先驅雅各布 • 伯努利（Jacob Bernoulli, 1654-1705）名字命名的、定義在0、1兩個符號構成的雙向序列符號空間上的「(1/2,1/2)-雙邊移位」和定義在0、1、2三個符號構成的雙向序列符號空間上的「(1/3,1/3,1/3)-雙邊移位」都具有數目和自然數一樣多的「勒貝格譜點」，因而它們兩兄弟是譜同構的。但數學家們一直弄不清楚它們是否也共軛，即：這兩個符號空間之間是否存在一個保測同構，使得一個位移與它的復合運算和它與另一個位移的復合運算結果完全是一碼事？1958年，正當遍歷理論家們為這個基本的未決問題絞盡腦汁之時，柯爾莫果洛夫剛剛產下了的「熵」馬上派上了大用場：他經過計算發現這兩個伯努利雙邊移位具有不同的熵值，前一個為 ln 2，後一個則為 ln 3，故它們不可能是共軛等價的。

大數學家的手一旦扭轉乾坤，共軛難題的一旦解決，熵馬上成了動力系統行家們爭相一抱的寵兒。很快，基於緊拓撲空間有限開覆蓋概念、用於探索連續函數迭代漸近性態的「拓撲熵」在柯爾莫果洛夫熵的思想指引下由西方數學鋪子的三大「鐵匠」 R. Adler, A. Konhein 和 M. McAndrew 鍛造出爐，並和柯爾莫果洛夫基於測度概念的「度量熵」密切相關，成為研究拓撲動力系統混沌性質的好工具。只要把緊拓撲空間的有限開覆蓋中的每個開子集看成所謂的波雷爾可測集，拓撲熵和柯爾莫果洛夫測度熵的數學推導過程頗為類似；文末參考文獻[1]給出了一個初等的推導。舉一個簡單的例子，著名的混沌映射之一「帽子函數」有拓撲熵 ln 2，它也等於其柯爾莫果洛夫熵。

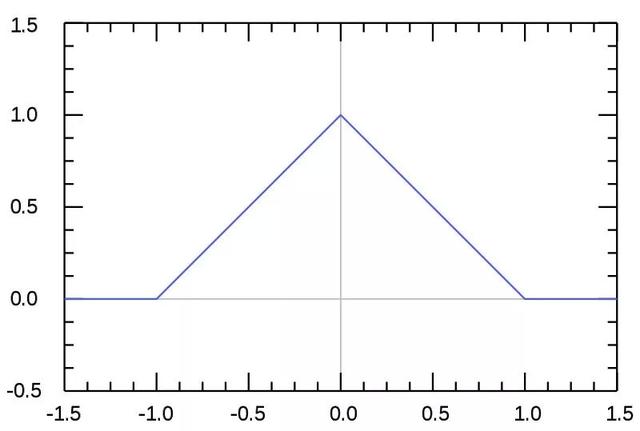
Hat function

3. 玻爾茲曼熵

玻爾茲曼熵可以看成是離散形式的香農熵在連續形式下的對等物。讓我們回憶一下，對應於有限樣本空間

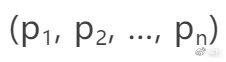
​的香農熵為

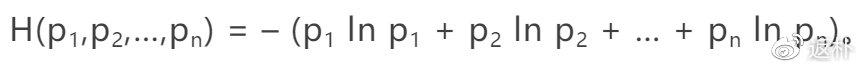
它看上去像某個被積函數的黎曼和。這引導我們走向定義一般密度函數的玻爾茲曼熵。為避免使用高深的測度論語言，我們只考慮 [0,1] 區間上的可積函數全體，用符號

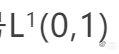
表示。這里的積分應該指的是數學系大三或大四才學的實變函數論里的勒貝格積分，但低年級的大學生可以把它想像成初等微積分中的黎曼積分；至少對連續的函數，這兩種積分是一樣的。可積的非負函數並且積分值為1則稱為密度函數。

1957年，美國物理學家埃德溫 • 傑恩斯（Edwin T. Jaynes, 1922-1998）在他分兩次發表、至今已被引用了將近12000次的論文《信息論與統計物理》[2] 中首次提出了「最大熵原則」。這個原則大致是說，當一個未知的概率密度函數的某些「可試驗信息」（例如有限多個的矩量或期望值）已知但卻不能唯一地確定該密度函數時，合理睬用的未知密度函數最佳逼近應是具有最大玻爾茲曼熵的那個密度函數，因它最不帶有「偏見」 (least biased)。根據最大熵定理，這個具有最大熵的密度函數不光是存在的，而且它可以通過矩量函數的某個線性組合與指數函數的復合函數，再標準化成一個密度函數來得到，只要這個特殊形式的密度函數具有和未知密度函數一模一樣的那些已知矩量值。

這樣一來，傑恩斯的最大熵原則成就了數值重獲未知密度函數的一個叫做「最大熵方法」的計算程式。事實上，六十年來，這是數學物理學家和工程師經常採用的一種「密度計算法」。傑恩斯終生在美國聖路易市華盛頓大學任教，1984年，物理系濃厚的最大熵氛圍熏陶出一位名叫勞倫斯 • 米德（Lawrence R. Mead, 1948-）的博士。退休前他和筆者在同一所大學執教並合寫過文章，是個很會教書、獲得過兩次校級教學獎的物理教授。米德一生中最有名的研究工作大概就是獲得博士學位那年在《數學物理雜誌》上發表的一篇合作論文[3]，至今為止每年都有不少人引用。在這篇題為《矩量問題中的最大熵》的文章里，作者證明了最大熵方法的弱收斂性，而這種收斂性對於物理學家考慮的許多問題來說已經是綽綽有餘了。數學家則感到不夠勁，於是就有兩位加拿大的數學家喬納森 • 博旺（Jonathan M. Borwein, 1951-）和艾德里安 • 劉易斯（Adrian S. Lewis, 1962-）在九十年代初嚴格證明了最大熵方法的強收斂。

在最大熵方法中，傳統的做法基本上是用單項式

來計算密度函數的對應矩量，但在計算數學家的眼里，這是代價極大的數值處理，因為算法極不穩定，用數值代數學家的行話說就是「條件數太大了」。難怪物理學家們能用到十來個矩量就感覺不得了了。對孜孜以求數值收斂性的計算數學家們來說，這怎麼能過癮呢。於是，一個新的想法[4]應運而生：把有限元的逐段多項式思想與最大熵原則相結合。這個算法借用了有限元空間基底函數「一的分解」的好性質，第一次用到與混沌有關的「不變密度函數」的數值計算上，條件數出奇地小，並且用到一百個甚至一千個矩量值也不在話下。

如今，五花八門的熵：信息熵、度量熵、拓撲熵、玻爾茲曼熵，加上定量刻畫「對初始條件敏感性」的李亞普洛夫（Alexandre Mikhailovich Liapunov, 1857-1918, 俄國數學家，以微分方程穩定性理論著稱於世）指數，再加上遍歷性、混合性、可遞性等用統計觀點看混沌的基本概念，一起組成了混沌、分形領域里克敵制勝的十八般兵器。

參考文獻

[1] 「Entropy – an introduction,」 Jiu Ding and Tien-Yien Li, NankaiSeries in Pure and Applied Mathematics and Theoretical Physics, Volume 4, WorldScientific, 26-53, 1993.

[2] Information theory and statistical physics, Physics Review 106(4), 620-630, 1957; Information theory and statistical physics, Physics Review 108(2), 171-190, 1957

[3] L.R. Mead and N. Papanicolaou, Maximum entropy in the problem of moments, J. Math. Phys. 25, 2404–2417, 1984.

[4] J. Ding, C. Jin, N. Rhee, and A. Zhou, “A maximum entropy method based on piecewise linear functions for the recovery of a stationary density of interval mappings,’’ J. Stat. Phys. 145, 1620-1639, 2011.

版權聲明：本文由《返樸》原創，歡迎個人轉發，嚴禁任何形式的媒體未經授權轉載和摘編。

《返樸》，致力好科普。國際著名物理學家文小剛與生物學家顏寧聯袂擔任總編，與幾十位學者組成的編委會一起，與你共同求索。關注《返樸》（微信號：fanpu2019）參與更多討論。二次轉載或合作請聯繫[email protected]。

特別提示：「返樸」正在求賢，有意者請戳「求賢」聯繫我們，等你來哦！​​​​

‘,