尋夢新聞LINE@每日推播熱門推薦文章,趣聞不漏接

里約熱內盧的高樓與貧民窟
導語
每一座繁華城市的角落里,都有人口稠密的貧民窟,在中國則是棚戶區。如何有效改善這些偏僻區域的環境狀況?最近發表在 Science Advances 上的一項研究表明,不必上演大規模強制拆遷的鬧劇,或許對城市街道的小小改造,就可以讓貧民區環境大大改觀!
全世界大約有 40 億人口生活在城市,然而其中接近四分之一的人口生活在城市中的貧民區。如果沒有切實可行的方案來解決這一問題,依照聯合國人居署(UN-Habitat)可能,到 2050 年,將有 64 億人生活在城市,而其中卻可能有 30 億人生活在貧民區。
推動可持續的城市化進程,關鍵在於改造乃至消除城市中的貧民區。然而,即便有相關的政策與資金支持,想改變貧民區的面貌,仍然面臨著來自環境、社會、經濟等多方面的壓力。
不過今年,來自美國能源部橡樹嶺國家實驗室、薩姆休斯頓州立大學以及芝加哥大學的研究人員,在 Science Advances 上發表了一篇論文,他們設計了新的數學模型,該模型力求通過最小成本的道路改造來提升局部交通條件,從而幫助城市貧民區和偏遠街區改變風貌。
橡樹嶺實驗室的研究員、該論文的主要作者 Christa Brelsford,認為這項研究可以改變貧民窟的未來。她表示,這項研究可以改善貧民窟人們的生活,這樣做有利於國家安全,因為越多人的基本需求能夠得到滿足,我們的生活就越有保障,越安全。
論文題目:
Toward cities without slums: Topology and the spatial evolution of neighborhoods
http://advances.sciencemag.org/content/advances/4/8/eaar4644.full.pdf
1. 難題: 城市規劃設計
雖然全球城市的增長、貧困現象的加劇,其規模和範圍都前所未有,但這並不是問題的本質。問題是具體的。
對於貧民窟和非正式定居點而言,雜亂無章的住房布局,會導致該區域缺乏足夠空間去建設規範的市政服務網路(例如水、電、燃氣管網和環衛設施)和寬闊的道路。在貧民窟里,想獲得乾淨的水、醫療服務等,都是困難的,甚至連醫療救援車輛、消防應急車輛也無法進入。
這帶來的後果可能很嚴重,比如:在缺乏電力設施的街區,居民會私拉電線、違規用電,而這又帶來了火災隱患,倘若火險出現,當地可能既缺乏消防設施,又因道路狹窄而無法獲得消防車輛救援,從而引發災難。
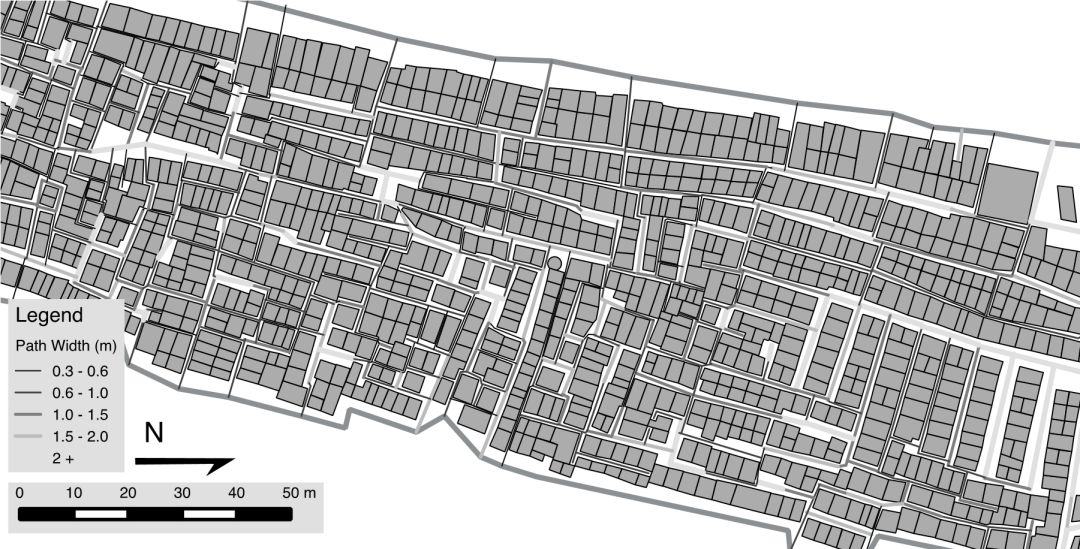
印度孟買某處的道路寬度示意圖
在印度孟買的一些街區里,雖然道路四通八達,但很多路其實非常狹窄。如上圖所示,大量道路寬度連1米都不到。糟糕的道路,妨礙了基礎設施的修建,妨礙了應急車輛和工程車輛的通行。
傳統的城市設計通常著眼於美學上是否吸引人,但卻難以進行定量的分析研究,其成功經驗的參考價值不足。
而該項目的研究者採用了一種新思路:不再依賴於傳統的幾何分析,而應用拓撲幾何的方法分析貧困和欠發達的城市街區。據此,他們發現了身處這些貧民區和非正式定居點時,獲取生活必需品和使用城市基礎設施的障礙所在。
2. 簡化: 城市拓撲結構

拓撲學也被稱作 「橡皮泥的幾何」,這個學科主要研究物體在連續變形的情況下,哪些性質保持不變,即拓撲不變性。

四座城市街區的拓撲變換
城市也具有拓撲不變性。上圖中展示了從紐約市的27個街區,到拉斯維加斯,到薩默林再到印度孟買貧民窟 Dharavi 之間的連續轉變。如動畫顯示,任何具有相同區塊數量(上圖是27個)的城市都可以「無縫切換」。這和一個杯子變成一個圓環的道理是一樣的。對於城市而言,這種相同的區塊數是拓撲變換中會被保留不變的部分。
站在這個視角,研究者推導出了城市的通用拓撲結構。
研究者將城市建築空間分為兩類:管網系統(access systems,如道路、市政管網)和 場所(places ,如建築物、公共空間)。這兩種類型的建築互相連接跨越了整個城市。研究者把城市分割為街區,每個街區都由通道相連。
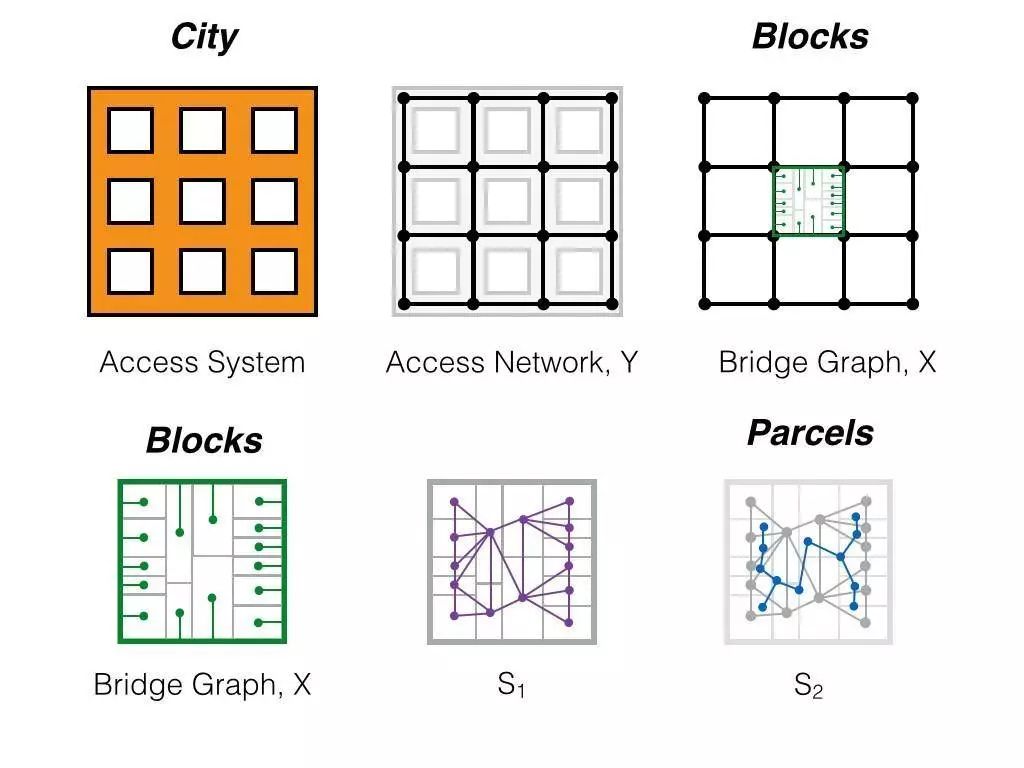
上圖表示了如何對一個城市進行拓撲分析:將城市的管網系統(access systems),簡化成數學上的拓撲網路,而一個區塊(Block)場所就位於網路中,通過橋(bridge)與管網系統相連。
進而,可以畫出每一個區塊的紫色、藍色兩層對偶圖(dual graph)。藍色圖的頂點位於紫色圖劃分出的面內,故名「對偶」,因不包含外部的空白區域,所以藍色圖 S2 是紫色圖 S1 的對偶圖的子圖,即弱對偶圖(Weak dual graph)。
對城市的管網系統(access systems)我們可以這樣做簡化:
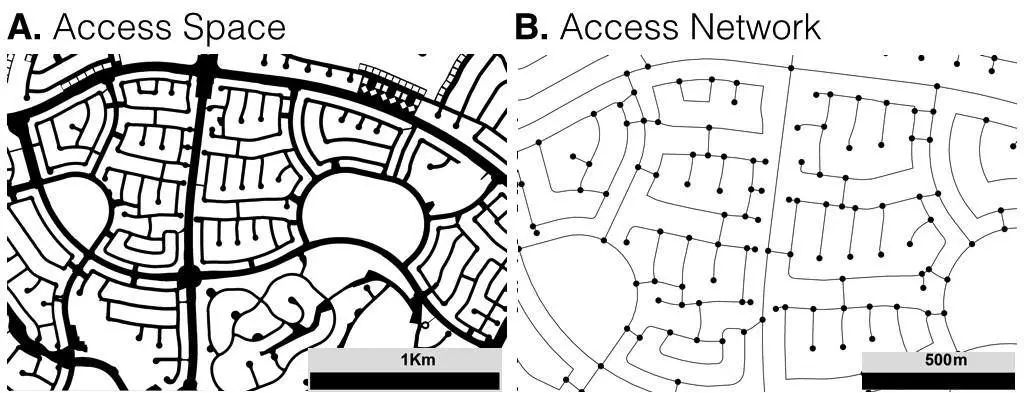
首先,如上圖所示,可以把拉斯維加斯的市政連接網路從左邊的實體地圖簡化為右邊的「圖」(Graph),二者的結構是一樣的。
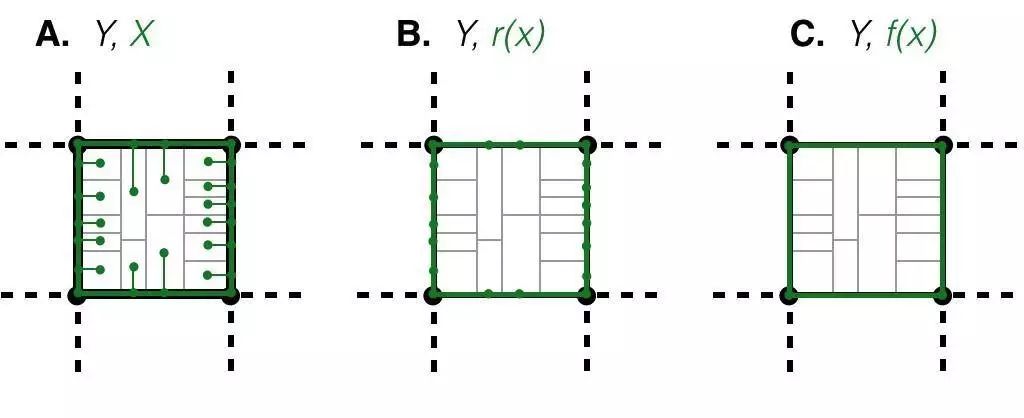
而在管網系統與場所連接的地方,如上圖表示,這個提供連接的橋(bridge)結構也是可以「縮回」的。經過這樣拓撲簡化,我們可以按照下文所示的分析方法,分析城市街區。
3. 分析: 區塊複雜度與連通性
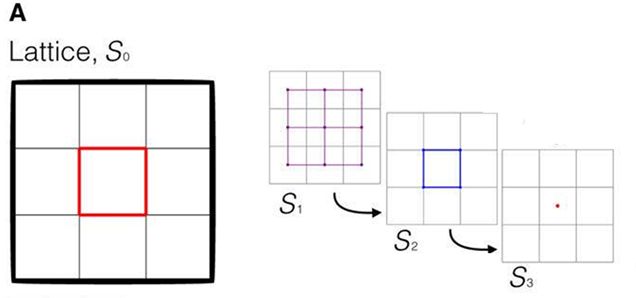
圖 A 表示的是一個理想的街區,表示原始的 圖S0。紫色的 圖S1是 圖S0 的弱對偶圖。藍色的 圖S2 是 圖S1 的弱對偶圖。以此層層嵌套,紅色的 圖S3(只有一個頂點)是 圖S2 的弱對偶圖。
這里的圖(Graph)指的是數學意義上由頂點和邊構成的圖。
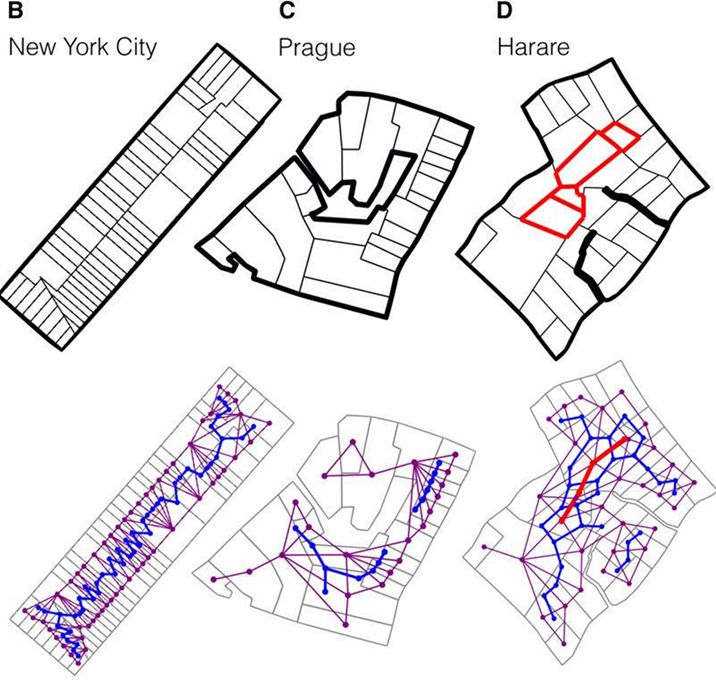
由此,我們來分析一下(B)紐約,(C)布拉格,和(D)哈拉雷三個城市的空間拓撲性質。
我們可以發現紐約和布拉格在拓撲分析中都只有兩層(紫色和藍色)弱對偶圖。而津巴布韋的哈拉雷有三層。這個最深的對偶圖層數在文中被稱為區塊復雜度(block complexity ),哈拉雷的區塊複雜度是 3。
一個城市街區的複雜度越大,也就意味著該區域與其他城市道路、水電管網系統連接越弱。城市中的貧民區,往往是區塊複雜度大的地方。
研究者發現當 圖S2 是樹(tree)形結構,即不再有環(loop)時,拓撲結構非常簡單,沒有下一層的弱對偶圖。比如上面的紐約和布拉格的 圖S2 都是樹形結構,其拓撲結構較為簡單,區塊複雜度低。而哈拉雷的 圖S2 結構中包含了環,所以還能形成下一層的弱對偶圖 S3。
拓撲不變性只約束了基本的函數關係,保留了相當大的幾何自由度。在研究者研究城市時,利用拓撲學把連通性定義為:管網系統(access systems,如道路、市政管網)和 場所 (places ,如建築物、公共空間)之間的一種基本空間關係。街區複雜度越低,連通性就越好。
由此構建的分析工具有助於識別出那些欠規劃、連通性低的地區,並能夠針對相關問題進一步的提出有效的建議。
4. 改造: 要想富,先修路
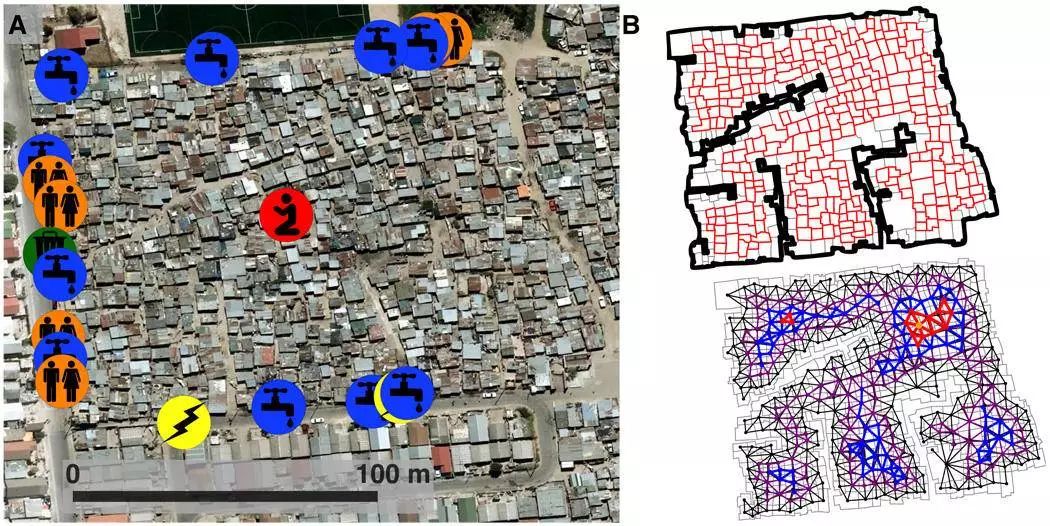
一個混亂街區的航拍圖、平面結構和拓撲結構
上圖展示了南非開普敦市 Khayelitsha 地區的一個非正規定居點,該定居點很有代表性——城市提供的公共管網設施,如水、電、廁所、垃圾回收站等,基本位於街區周邊的街道上,而位於內部中心的公共設施只有一個宗教場所。
這個大街區的內部結構,如右上圖的紅色方框所示,右下圖是它層層嵌套的弱對偶圖。按照前文的分析方法,可以算出這個街區的區塊複雜度是 9,相當複雜。
通過這樣的拓撲分析,研究者可以分析任何城市,並能找到缺乏通道的場所,並提出修建道路管網的解決方案,以最低的成本解決問題。這樣就可以通過盡量小的改變來獲盡可能大的改進提升。
以津巴布韋的哈拉雷為例,我們通過修建簡短的幾條路徑就能解決中心區域的連通性問題。但是這樣的修路方式也有待進一步提高:修建的都是死胡同,不符合我們觀念中的道路應四通八達的印象。
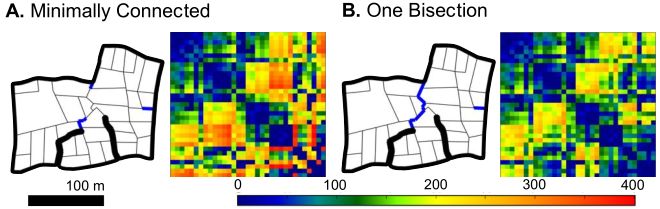
哈拉雷某街區改造前(A)後(B)對比
以哈拉雷的一個街區為例(上圖),我們可以看到,只需要修建簡短的幾條路徑,就能解決中心區域的連通性問題——
用熱力圖來表示任意兩點之間通行所需距離,顏色越紅表示距離越遠。從 A 到 B,僅僅是修通了一條貫穿街區內部的小路,就能夠顯著降低街區中所有點位之間的平均通行距離。
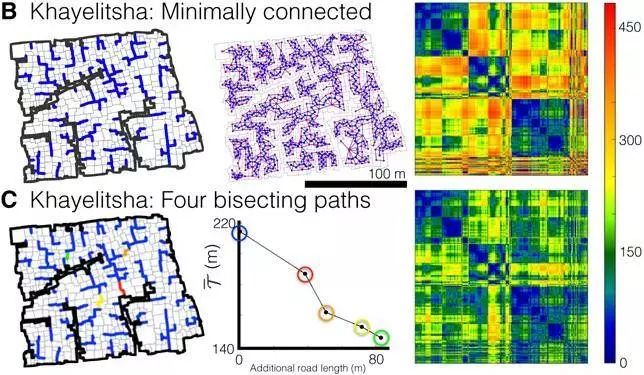
開普敦 Khayelitsha 某街區改造前(B)後(C)對比
再以前文 Khayelitsha 地區的這個混亂街區為例,本來該街區的連通性非常差,區塊複雜度高達9。在原始道路 B 中,任意兩點之間通行的距離普遍較長,達到了220米,通行距離熱力圖的顏色也偏紅。
有沒有減小平均通行距離、降低通行成本的辦法呢?有,只需要修四條小路。
在補充了紅、黃、橙、綠四條短路之後(圖 C),街區所有點位之間的平均通行距離從 220 米降低到了 140 米。要知道這四條路的總長也不過只有 80 米!
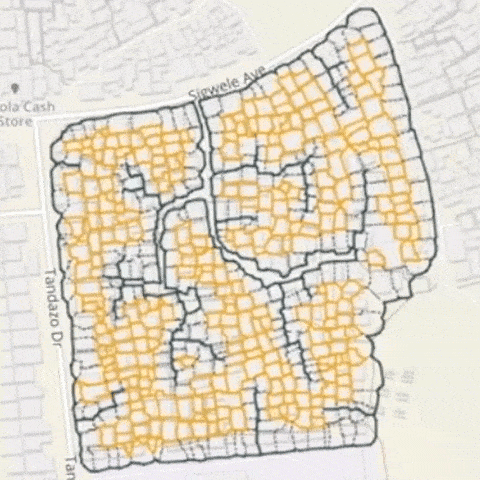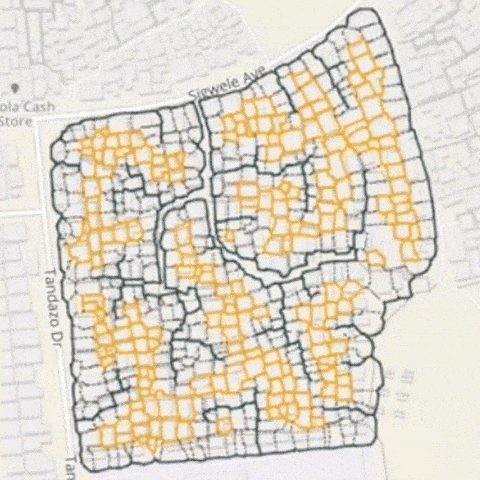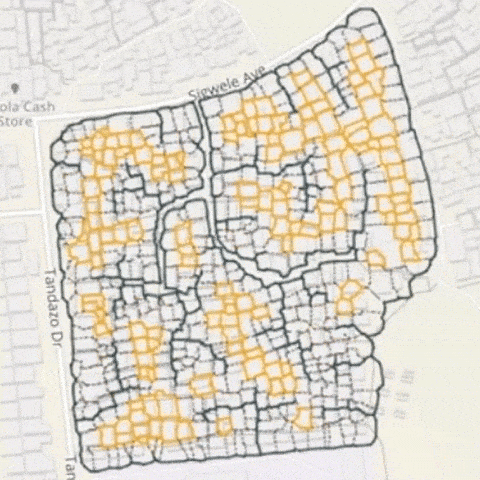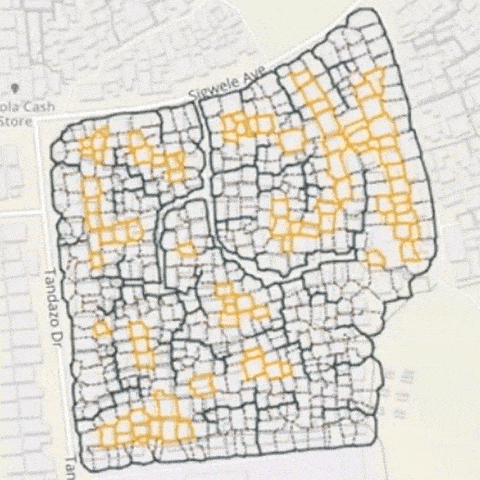
上圖是南非開普敦貧民窟改造項目全貌。深色的線表示道路。橙色圈起來的,表示沒有與市政管網直接相連的街區。
芝加哥大學 Mansueto 城市創新研究所所長、論文合著者 Luís Bettencourt認為,通過理解基本的拓撲結構——居住地、工作地與城市基礎設施網路之間的關係——我們可以確定城市中的哪些部分仍然相對孤立。通過極少的干預,就能完成繪圖、測量、求解等工作,以此規劃解決方案,創造具備歷史特色且以人為本的新城市。
這篇論文的研究成果已經應用於南非開普敦和印度孟買這兩座城市。人們通過拓撲分析識別出複雜度高的街區,從而有針對性地修建道路,這樣就能高效地改善城市中落後地區的交通狀況,進而促進經濟發展。
要想富,先修路。多一些對城市道路的小小改造,就會少一些沸沸揚揚的強拆、趕人鬧劇。
參考資料
http://advances.sciencemag.org/content/4/8/eaar4644
https://www.youtube.com/watch?v=ISAKisBQMoo
https://www.eurekalert.org/pub_releases/2018-08/drnl-mca082418.php
https://www.eurekalert.org/pub_releases/2018-08/aaft-att082718.php
https://openreblock.org/capetown.html
作者:Leo、劉培源
編輯:王怡藺
審核通過後,我們將以郵件、簡訊或微信等方式通知您
商務合作及投稿轉載|[email protected]
◆ ◆ ◆









