大數據學習之初學者必知的十大算法

本文先為初學者介紹了必知的十大機器學習（ML）算法，並且我們通過一些圖解和實例生動地解釋這些基本機器學習的概念。我們希望本文能為理解機器學習基本算法提供簡單易讀的入門概念。本文轉載自科多大數據

機器學習模型

在《哈佛商業評論》發表「數據科學家是 21 世紀最性感的職業」之後，機器學習的研究廣受關注。所以，對於初入機器學習領域的學習者，我們放出來一篇頗受歡迎的博文——《初學者必知的十大機器學習算法》，盡管這只是針對初學者的。

機器學習算法就是在沒有人類干預的情況下，從數據中學習，並在經驗中改善的一種方法，學習任務可能包括學習從輸入映射到輸出的函數，學習無標籤數據的隱含結構；或者是「基於實例的學習」，通過與存儲在記憶中的訓練數據做比較，給一個新實例生成一個類別標籤。基於實例的學習（instance-based learning）不會從具體實例中生成抽象結果。

機器學習算法的類型

有三類機器學習算法：

可以這樣來描述監督學習：使用有標籤的訓練數據去學習從輸入變量（X）到輸出變量（Y）的映射函數。

Y = f (X)

它分為兩種類型：

a. 分類：通過一個給定的輸入預測一個輸出，這里的輸出變量以類別的形式展示。例如男女性別、疾病和健康。

b. 回歸：也是通過一個給定的輸入預測一個輸出，這里的輸出變量以實數的形式展示。例如預測降雨量、人的身高等實數值。

本文介紹的前 5 個算法就屬於監督學習：線性回歸、Logistic 回歸、CART、樸素貝葉斯和 KNN。

集成學習也是一種監督學習方法。它意味著結合多種不同的弱學習模型來預測一個新樣本。本文介紹的第 9、10 兩種算法–隨機森林 Bagging 和 AdaBoost 提升算法就是集成學習技術。

非監督學習問提僅僅處理輸入變量（X），但不會處理對應的輸出（也就是說，沒有標籤）。它使用無標籤的訓練數據建模數據的潛在結構。

非監督學習可以分為 2 種類型：

a. 關聯：就是去發覺在同一個數據集合中不同條目同時發生的概率。廣泛地用於市場籃子分析。例如：如果一位顧客買了麵包，那麼他有 80% 的可能性購買雞蛋。

b. 聚類：把更加相似的對象歸為一類，而不是其他類別對象。

c. 降維：顧名思義，降維就是減少數據集變量，同時要保證重要信息不丟失。降維可以通過使用特徵提取和特徵選擇方法來完成。特徵選擇方法會選擇原始變量的一個子集。特徵提取完成了從高維空間到低維空間的數據變換。例如，主成分分析（PCA）就是一個特徵提取方法。

本文介紹的算法 6-8 都是非監督學習的例子：包括 Apriori 算法、K-均值聚類、主成分分析（PCA）。

強化學習是這樣一種學習方法，它允許智能體通過學習最大化獎勵的行為，並基於當前狀態決定下一步要採取的最佳行動。

強化學習一般通過試錯學習到最佳行動。強化學習應用於機器人，機器人在碰到障礙物質之後會收到消極反饋，它通過這些消極反饋來學會避免碰撞；也用在視頻遊戲中，通過試錯發現能夠極大增長玩家回報的一系列動作。智能體可以使用這些回報來理解遊戲中的最佳狀態，並選擇下一步的行動

監督學習

在機器學習中，我們用輸入變量 x 來決定輸出變量 y。輸入變量和輸出變量之間存在一個關係。機器學習的目標就是去定量地描述這種關係。

線性回歸預測是連續值（如公分級的降雨量），logistic 回歸預測是使用了一種變換函數之後得到的離散值（如一位學生是否通過了考試）。

Logistic 回歸最適合於二元分類問題（在一個數據集中，y=0 或者 1，1 代表默認類。例如：在預測某個事件是否會發生的時候，發生就是 1。在預測某個人是否患病時，患病就是 1）。這個算法是拿它所使用的變換函數命名的，這個函數稱為 logistics 函數（logistics function，h(x)= 1/ (1 + e^x)），它的圖像是一個 S 形曲線。

在 logistic 回歸中，輸出是默認類別的概率（不像線性回歸一樣，輸出是直接生成的）。因為是概率，所以輸出的值域是 [0,1]。輸出值 y 是通過輸入值 x 的對數變換 h(x)= 1/ (1 + e^ -x) 得到的。然後使用一個閾值強制地讓輸出結果變成一個二元分類問題。

分類和回歸樹（CART）是決策樹的一種補充。

非終端節點（non-terminal node）包含根節點 (root node) 和中間節點 (internal node)。每一個非終端節點代表一個單獨的輸入變量 x 和這個變量的分支節點；葉節點代表的是輸出變量 y。這個模型按照以下的規則來作出預測：

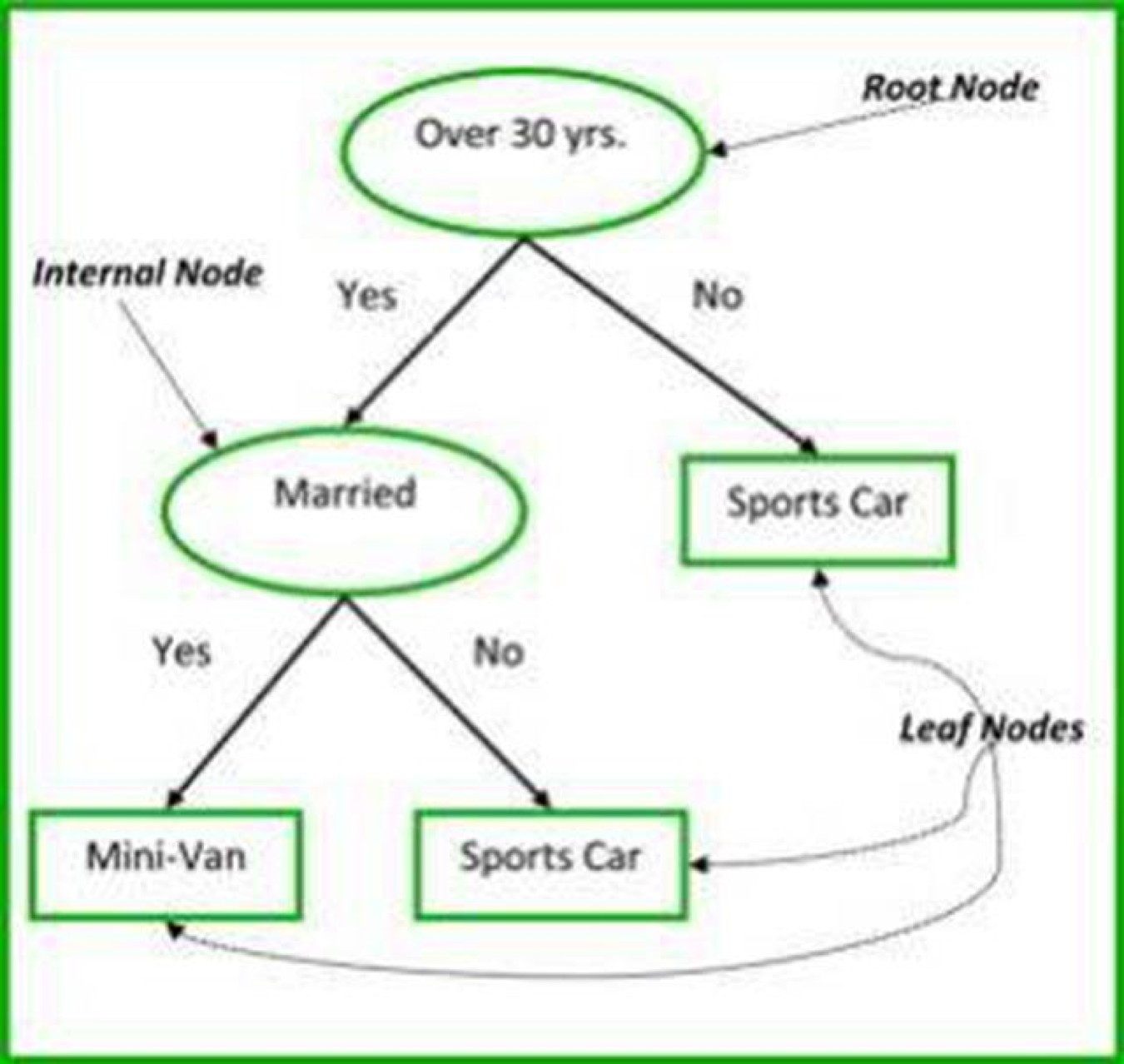
決策樹的一些部分

在給定一個早已發生的事件的概率時，我們用貝葉斯定理去計算某個事件將會發生的概率。在給定一些變量的值時，我們也用貝葉斯定理去計算某個結果的概率，也就是說，基於我們的先驗知識（d）去計算某個假設（h）為真的概率。計算方法如下：

P(h|d)= (P(d|h) * P(h)) / P(d)

其中，

• P(h|d) = 後驗概率。就是假設 h 為真概率，給定的數據相當於先驗知識 d。其中 P(h|d)= P(d1| h)* P(d2| h)*….*P(dn| h)* P(d)。

• P(d|h) = 似然度。假設 h 正確時，數據 d 的概率。

• P(h) = 類先驗概率。假設 h 正確的額概率。(無關數據)

• P(d) = 預測器先驗概率。數據的概率（無關假設)

這個算法被稱為「樸素」的原因是：它假設所有的變量是相互獨立的，這也是現實世界中做出的一個樸素的假設。

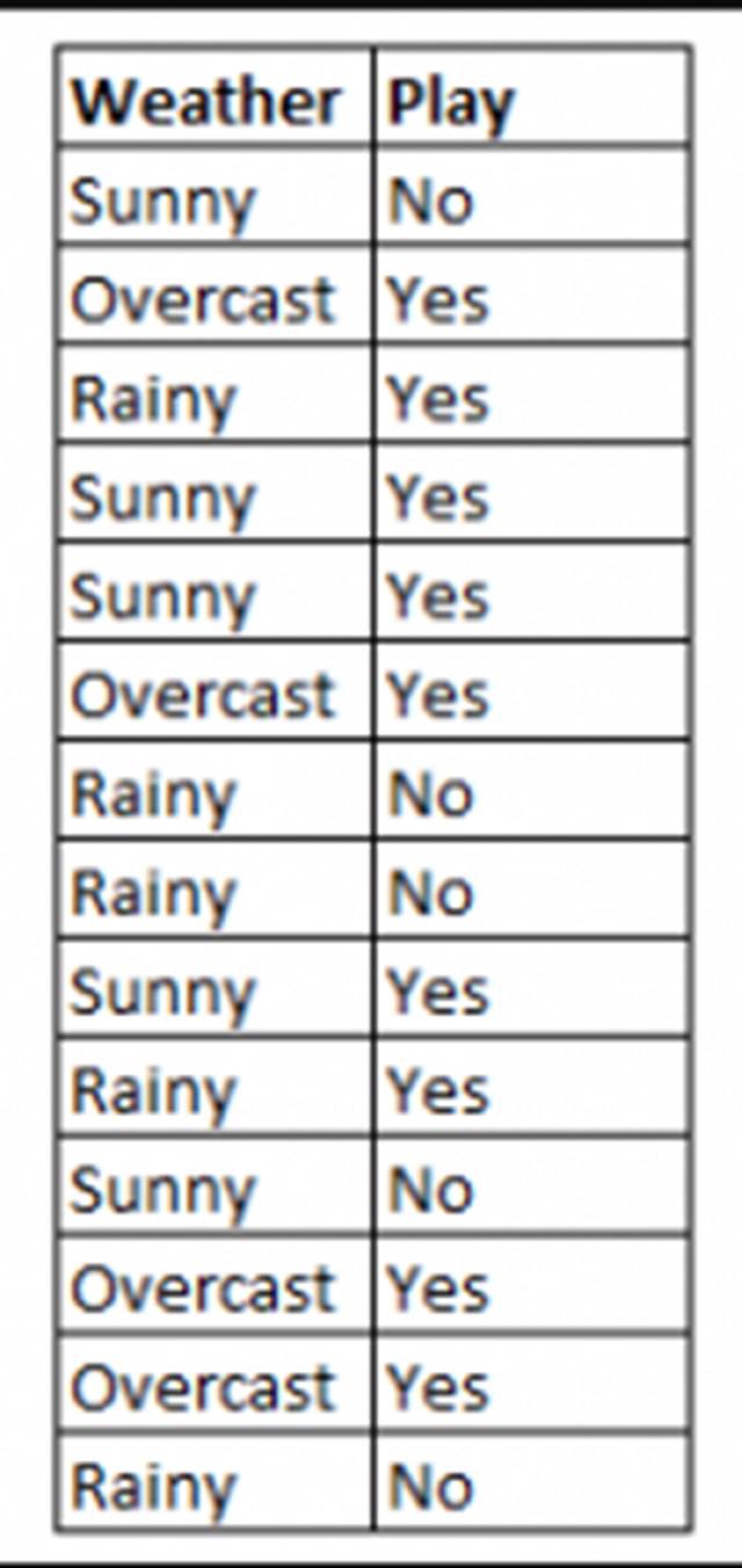
使用樸素貝葉斯法來預測變量「天氣」變化狀態

以上圖為例，如果天氣=晴天，那麼輸出是什麼呢？

在給定變量天氣=晴天時，為了判斷結果是或者否，就要計算 P(yes|sunny) 和 P(no|sunny)，然後選擇概率較大的結果。

計算過程如下：

->P(yes|sunny)= (P(sunny|yes) * P(yes)) / P(sunny) = (3/9 * 9/14 ) / (5/14) = 0.60 -> P(no|sunny)= (P(sunny|no) * P(no)) / P(sunny) = (2/5 * 5/14 ) / (5/14) = 0.40

所以，天氣=晴天時，結果為是。

KNN 使用了整個數據集作為訓練集，而不是將它分為訓練集和測試集。

當給定的一個數據實例時，KNN 算法會在整個數據集中尋找 k 個與其新樣本距離最近的，或者 k 個與新樣本最相似的，然後，對於回歸問題，輸出結果的平均值，或者對於分類問題，輸出頻率最高的類。k 的值是用戶自定義的。

樣本之間的相似性是用歐氏距離或者漢明（Hamming）距離來計算的。

非監督學習算法

Apriori 算法被用來在交易數據庫中進行挖掘頻繁的子集，然後生成關聯規則。常用於市場籃子分析，分析數據庫中最常同時出現的交易。通常，如果一個顧客購買了商品 X 之後又購買了商品 Y，那麼這個關聯規則就可以寫為：X -> Y。

例如：如果一位顧客購買了牛奶和甜糖，那他很有可能還會購買咖啡粉。這個可以寫成這樣的關聯規則： {牛奶，甜糖} -> 咖啡粉。關聯規則是交叉了支持度（support）和置信度（confidence）的閾值之後產生的。

支持度的程度幫助修改在頻繁的項目集中用來作為候選項目集的數量。這種支持度的衡量是由 Apriori 原則來指導的。Apriori 原則說明：如果一個項目集是頻繁的，那麼它的所有子集都是頻繁的。

K-均值是一個對相似的數據進行聚類的迭代算法。它計算出 k 個聚類的中心點，並給某個類的聚類分配一個與其中心點距離最近的數據點。

K-均值算法的步驟

步驟 1：K-均值初始化

a) 選擇一個 k 值。這里我們令 k=3。

b) 將數據點隨機地分配給三個聚類。

c) 計算出每個聚類的中心點。圖中的紅色、藍色和綠色的星分別代表三個聚類的中心點。

步驟 2：將每一個觀測值與一個聚類關聯起來

將每一個數據點重新分配給離它最近的一個聚類中心點。如圖所示，上邊的五個數據點被分配給了藍星代表的聚類。按照相同的步驟將數據點分配給紅色和綠色星代表的聚類中心點。

步驟 3：重新計算中心點

計算新聚類的中心點。如圖所示，舊中心點是灰色的，新中心點是紅色、藍色和綠色的。

步驟 4：迭代，然後在數據點所屬的聚類不變的時候退出整個過程

重復步驟 2-3，直至每一個聚類中的點不會被重新分配到另一個聚類中。如果在兩個連續的步驟中不再發生變化，那麼就退出 K-均值算法。

主成分分析（PCA）通過減少變量的數目來使數據變得更加易於探索和可視化。這通過將數據中擁有最大方差的數據抽取到一個被稱為「主成分」的新坐標系中。每一個成分都是原始變量的一個新的線性組合，且是兩兩統計獨立的。統計獨立意味著這些成分的相關係數是 0。

第一主成分捕獲的是數據中最大方差的數據。第二主成分捕獲的是剩下的數據中方差最大但是與第一主成分相互獨立的數據。相似地，後續的主成分（例如 PC3、PC4）都是剩下的數據中方差最大的但是與之前的主成分保持獨立的數據

集成意味著通過投票或者取平均值的方式，將多個學習器（分類器）結合起來以改善結果。在分類的時候進行投票，在回歸的時候求平均值。核心思想就是集成多個學習器以使性能優於單個學習器。有三種集成學習的方法：裝袋（Bagging）、提升（Boosting）和堆疊（Stacking）。本文不涉及堆疊。

隨機森林（多個學習器）是在裝袋決策樹（單個學習器）上做的改進。

Bagging：Bagging 的第一步就是在使用 Bootstrap 采樣方法得到的數據庫中創建多個模型，每個生成的訓練集都是原始數據集的子集。每個訓練集都有相同的大小，但是有些樣本重復出現了很多次，有些樣本一次未出現。然後，整個原始數據集被用為測試集。那麼，如果原始數據集的大小為 N，則每個生成的訓練集的大小也是 N，唯一（沒有重復）樣本的大小大約是 2*N/3；測試集的大小也是 N。

Bagging 的第二步就是使用同一個算法在不同的數據集上生成多個模型。然後，我們討論一下隨機森林。在決策樹中，每個節點都在最好的、能夠最小化誤差的最佳特徵上進行分支，而隨機森林與之不同，我們選擇隨機分支的特徵來構建最佳的分支。進行隨機處理的原因在於：即便使用了 Bagging，當決策樹選擇最佳特徵來分支的時候，它們最終會有相似的模型和相關聯的預測結果。但是用隨機子集上的特徵進行分支意味著子樹做的預測是沒有多少相關性的。

a）Bagging 是並行集成，因為每個模型都是獨立建立的。然而，提升是一個順序性集成，每個模型都要糾正前面模型的錯誤分類。

b）Bagging 主要涉及到「簡單投票」，每個分類器都投票得到一個最終結果，這個分類結果是由並行模型中的大多數模型做出的；提升則使用「權重投票」。每個分類器都會投票得到一個由大多數模型做出的結果—但是建立這些順序性模型的時候，給之前誤分類樣本的模型賦予了較大的權重。

Adaboost 指的是適應性提升。

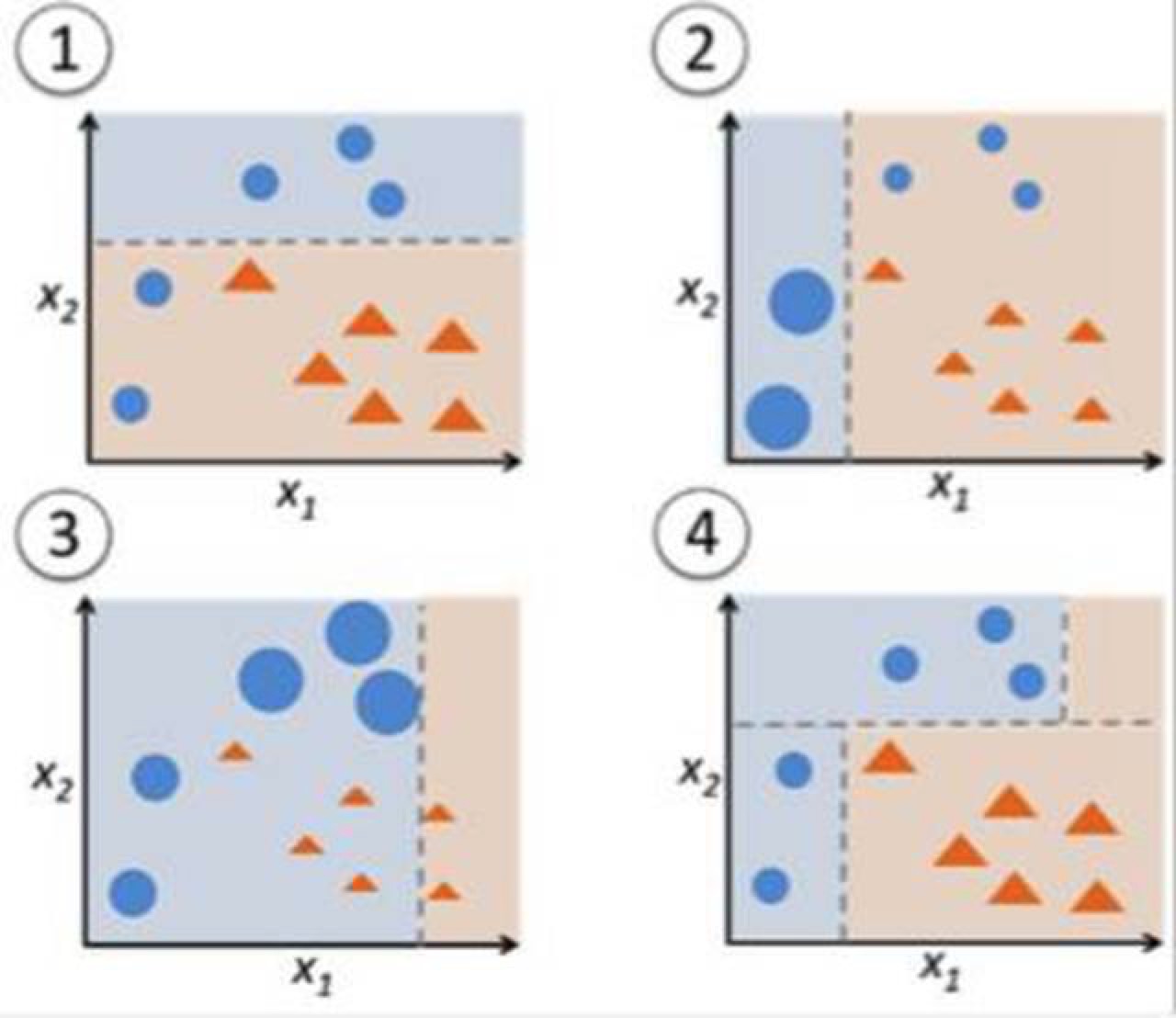
一個決策樹的 Adaboost

在上圖 中，步驟 1、2、3 指的是被稱為決策樁（decision stump）的弱學習器（是一個僅依靠一個輸入作出決策的 1 級決策樹；是一種根節點直接連接到葉節點的決策樹）。構造決策樹的過程會一直持續，直到用戶定義了一個弱學習器的數目，或者訓練的時候再也沒有任何提升的時候。步驟 4 結合了之前模型中的 3 個決策樁（所以在這個決策樹中就有 3 種分支規則）。

步驟 1：開始用 1 個決策樁來根據 1 個輸入變量做決策

數據點的大小說明我們應用了等權重來將它們分為圓形或者三角形。決策樁在圖的上半部分用一條水平線來對這些點進行分類。我們可以看到，有兩個圓被誤分為三角形。所以，我們會賦予這兩個圓更大的權重，然後使用另一個決策樁（decision stump）。

步驟 2：轉向下一個決策樁，對另一個輸入變量進行決策

我們可以看到，之前的步驟中誤分類的兩個圓要比其餘數據點大。現在，第二個決策樁要嘗試正確地預測這兩個圓。

賦予更大權重的結果就是，這兩個圓被左邊的豎線正確地分類了。但是這又導致了對上面 3 個小圓的誤分類。因此，我們要在另一個決策樁對這三個圓賦予更大的權重。

步驟 3：訓練另一個決策樁對下一個輸入變量進行決策。

上一步誤分類的 3 個圓要比其他的數據點大。現在，在右邊生成了一條豎線，對三角形和圓進行分類。

步驟 4：結合決策樁

我們結合了之前 3 步的決策樁，然後發現一個複雜的規則將數據點正確地分類了，性能要優於任何一個弱學習器。

結語

回顧一下，本文主要學到的內容：

1 5 種監督學習技術：線性回歸、Logistic 回歸、CART（分類和決策樹）、樸素貝葉斯法和 KNN。

2 3 種非監督學習技術：Apriori 算法、K-均值聚類、主成分分析（PCA）。

3 兩種集成學習方法：Bagging 隨機森林、AdaBoost 提升。

綜上所述，機器學習的基本屬性可以總結為以下：

• 機器學習是（使用樣本獲取近似函數的）統計學的一個分支。我們有一個確實存在的理論函數或分布用以生成數據，但我們目前不知道它是什麼。我們可以對這個函數進行抽樣，這些樣本選自我們的訓練集。

• 以圖片描述任務為例：函數：f⋆（圖片）→圖片描述，樣本：data∈（image，deion）。注意：由於一個物體有許多有效的描述，所以描述是文本空間中的一個分布：圖片描述〜文本。

機器的目標是找到模型：有足夠的表現力來逼近真正的函數，找到一個高效的算法，它使用訓練數據找到函數最優解。而且此最優解必須對未知輸入有良好的泛化能力。